题目内容
【题目】如图,在直角坐标系xoy中,其中A(0,0),B(2,0),C(1,1),D(0,1),图中圆弧所在圆的圆心为点C,半径为 ![]() ,且点P在图中阴影部分(包括边界)运动.若
,且点P在图中阴影部分(包括边界)运动.若 ![]() ,其中
,其中 ![]() ,则
,则 ![]() 的取值范围是( )
的取值范围是( )
A.[2,3+ ![]() ]
]
B.[2,3+ ![]() ]
]
C.[3- ![]() , 3+
, 3+ ![]() ]
]
D.[3- ![]() , 3+
, 3+ ![]() ]
]
【答案】B
【解析】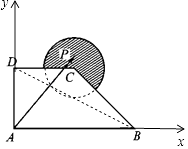
以A为坐标原点,AB为x轴,DA为y轴建立平面直角坐标系则
A(0,0),D(0,1),C(1,1),B(2,0)
直线BD的方程为x+2y﹣2=0,C到BD的距离d= ![]() ;
;
∴以点C为圆心,以 ![]() 为半径的圆方程为(x﹣1)2+(y﹣1)2=
为半径的圆方程为(x﹣1)2+(y﹣1)2= ![]() ,
,
设P(m,n)则 ![]() =(m,n),
=(m,n), ![]() =(2,0),
=(2,0), ![]() =(﹣1,1);
=(﹣1,1);
∴(m,n)=(2x﹣y,y)
∴m=2x﹣y,n=y,
∵P在圆内或圆上
∴(2x﹣y﹣1)2+(y﹣1)2≤ ![]() ,
,
设4x﹣y=t,则y=4x﹣t,代入上式整理得
80x2﹣(48t+16)x+8t2+7≤0,
设f(x)=80x2﹣(48t+16)x+8t2+7,x∈[ ![]() ,
, ![]() ],
],
则 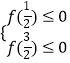 ,
,
解得2≤t≤3+ ![]() ,
,
∴4x﹣y的取值范围是[2,3+ ![]() ].
].
所以答案是:B
【考点精析】利用平面向量的坐标运算和圆的标准方程对题目进行判断即可得到答案,需要熟知坐标运算:设![]() ,
,![]() 则
则![]() ;
;![]() ;设
;设![]() ,则
,则![]() ;圆的标准方程:
;圆的标准方程:![]() ;圆心为A(a,b),半径为r的圆的方程.
;圆心为A(a,b),半径为r的圆的方程.

【题目】某中学调查了某班全部 45 名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)
参加书法社团 | 未参加书法社团 | |
参加演讲社团 | 8 | 5 |
未参加书法社团 | 2 | 30 |
(1)从该班随机选 1 名同学,求该同学至少参加上述一个社团的概率;
(2)在既参加书法社团又参加演讲社团的 8 名同学中,有 5 名男同学![]() ,3名女同学
,3名女同学![]() .现从这 5 名男同学和 3 名女同学中各随机选 1 人,求
.现从这 5 名男同学和 3 名女同学中各随机选 1 人,求![]() 被选中且
被选中且![]() 未被选中的概率.
未被选中的概率.