题目内容
命题:(1)若f(x)=ax2+bx+3a+b是偶函数,其定义域是[a-1,2a],则f(x)在区间
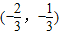 是减函数.
是减函数.(2)如果一个数列{an}的前n项和
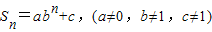 则此数列是等比数列的充要条件是a+c=0.
则此数列是等比数列的充要条件是a+c=0.(3)曲线y=x3+x+1过点(1,3)处的切线方程为:4x-y-1=0.
(4)已知集合P∈{(x,y)|y=k},Q∈{(x,y)|y=ax+1,a>0且a≠1},若P∩Q只有一个子集.则k<1.
以上四个命题中,正确命题的序号是 .
【答案】分析:根据函数奇偶性的定义和二次函数单调性的结论,得到(1)正确;根据等比数列的通项与性质,结合已知Sn求的an方法,通过正反论证可得(2)正确;曲线y=x3+x+1过点(1,3)处的切线方程为:4x-y-1=0或7x-4y+3=0,故(3)不正确;p∩Q只有一个子集,说明p∩Q是空集,集合Q中,y=ax+1>1,(a>0且a≠1)故k≤1时,P∩Q=∅,故(4)不正确.
解答:解:(1)∵偶函数的定义域关于原点对称,
∴a-1+2a=0,a= ,
,
∵f(x)=ax2+bx+3a+b是偶函数,∴b=0,
∴f(x)=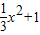 ,
,
∴f(x)在区间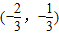 是减函数,故(1)正确;
是减函数,故(1)正确;
(2)数列{an}的前n项和Sn=abn+c,
可得当n≥2时,an=Sn-Sn-1=abn-1(b-1),
当n=1时,a1=S1=ab+c,
接下来讨论充分性与必要性,
若a+c=0,则ab+c=a(b-1)=ab1-1(b-1),
可得数列的通项为an=a(b-1)bn-1,
∵a≠0,b≠0,b≠1,
∴数列{an}构成以a(b-1)为首项,公比为b的等比数列.故充分性成立;
反之,若此数列是等比数列,得
∵当n≥2时,an=abn-1(b-1),公比为b
∴a2=ab1(b-1)=ba1=b(ab+c)
∴-ab=bc⇒b(a+c)=0
∵b≠0,
∴a+c=0,故必要性成立,说明(2)正确;
(3)∵y=x3+x+1,∴y′=3x2+1,
∴y=x3+x+1在(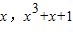 )处的切线方程为:
)处的切线方程为:
y-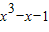 =(3
=(3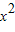 +1)(x-x),
+1)(x-x),
∵点(1,3)在切线上,
∴3-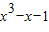 =(3
=(3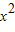 +1)(1-x),
+1)(1-x),
解得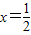 ,或x=1,
,或x=1,
∴曲线y=x3+x+1过点(1,3)处的切线方程为:4x-y-1=0或7x-4y+3=0,故(3)不正确;
(4)p∩Q只有一个子集,说明p∩Q是空集,
集合Q中,y=ax+1>1,(a>0且a≠1)
故k≤1时,P∩Q=∅,故(4)不正确.
故答案为:(1)(2).
点评:本题考查命题的真假判断,解题时要认真审题,注意函数性质、等比数列、切线方程、集合等知识点的灵活运用.
解答:解:(1)∵偶函数的定义域关于原点对称,
∴a-1+2a=0,a=
 ,
,∵f(x)=ax2+bx+3a+b是偶函数,∴b=0,
∴f(x)=
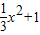 ,
,∴f(x)在区间
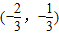 是减函数,故(1)正确;
是减函数,故(1)正确;(2)数列{an}的前n项和Sn=abn+c,
可得当n≥2时,an=Sn-Sn-1=abn-1(b-1),
当n=1时,a1=S1=ab+c,
接下来讨论充分性与必要性,
若a+c=0,则ab+c=a(b-1)=ab1-1(b-1),
可得数列的通项为an=a(b-1)bn-1,
∵a≠0,b≠0,b≠1,
∴数列{an}构成以a(b-1)为首项,公比为b的等比数列.故充分性成立;
反之,若此数列是等比数列,得
∵当n≥2时,an=abn-1(b-1),公比为b
∴a2=ab1(b-1)=ba1=b(ab+c)
∴-ab=bc⇒b(a+c)=0
∵b≠0,
∴a+c=0,故必要性成立,说明(2)正确;
(3)∵y=x3+x+1,∴y′=3x2+1,
∴y=x3+x+1在(
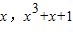 )处的切线方程为:
)处的切线方程为:y-
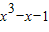 =(3
=(3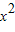 +1)(x-x),
+1)(x-x),∵点(1,3)在切线上,
∴3-
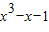 =(3
=(3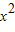 +1)(1-x),
+1)(1-x),解得
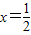 ,或x=1,
,或x=1,∴曲线y=x3+x+1过点(1,3)处的切线方程为:4x-y-1=0或7x-4y+3=0,故(3)不正确;
(4)p∩Q只有一个子集,说明p∩Q是空集,
集合Q中,y=ax+1>1,(a>0且a≠1)
故k≤1时,P∩Q=∅,故(4)不正确.
故答案为:(1)(2).
点评:本题考查命题的真假判断,解题时要认真审题,注意函数性质、等比数列、切线方程、集合等知识点的灵活运用.

练习册系列答案
相关题目