题目内容
某生产流水线,由于改进了设备,预计第一年产量的增长率为160%,以后每年的增长率是前一年的一半.设原来的产量是a.
(Ⅰ)写出改进设备后的第一年,第二年,第三年的产量,并写出第n年与第n-1年(n≥2,n∈N)的产量之间的关系式;
(Ⅱ)由于设备不断老化,估计每年将损失年产量的5%,如此下去,以后每年的产量是否始终是逐年提高?若是,请给予证明;若不是;请说明从第几年起,产量将比上一年减少?
答案:
解析:
解析:
|
解:(Ⅰ)设第n年的产量为an,则 a1=a(1+160%), a2=a(1+160%)(1+80%), a3=a(1+160%)(1+80%)(1+40%), …… 即a1= ∴an=an-1(1+ (Ⅱ)依题意,an=an-1(1+ 若以后每年的产量逐年减少,即an<an-1,也即(1+ ∴1+ ∴当n-4≥2,即n≥6时,an<an-1 故从第6年起,产量比上一年减少. |

练习册系列答案
相关题目
 a,a=
a,a=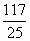 a,a3=
a,a3=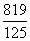 a.
a.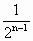 ×160%)=an-1(1+
×160%)=an-1(1+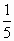 ×
×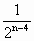 )(n≥2,n∈N).
)(n≥2,n∈N).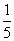 ×
×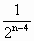 )(1-5%).
)(1-5%).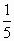 ×
×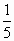 ×
×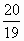 ,即2n-4>
,即2n-4>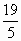 . 但22>
. 但22>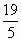 ,21<
,21<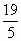 ,且n≥2,n∈N,
,且n≥2,n∈N, (k为常数),如果不搞促销活动,该产品的年销售量只能是1万件,已知2003年生产该产品的固定投入为8万元,每生产1万件该产品需要投入16万元,厂家将每件产品的销售价格定为年平均每件产品成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
(k为常数),如果不搞促销活动,该产品的年销售量只能是1万件,已知2003年生产该产品的固定投入为8万元,每生产1万件该产品需要投入16万元,厂家将每件产品的销售价格定为年平均每件产品成本的1.5倍(产品成本包括固定投入和再投入两部分资金).