题目内容
给出以下命题:①函数
 既无最大值也无最小值;
既无最大值也无最小值;②函数f(x)=|x2-2x-3|的图象关于直线x=1对称;
③若函数f(x)的定义域为(0,1),则函数f(x2)的定义域为(-1,1);
④若函数f(x)满足|f(-x)|=|f(x)|,则函数f(x)或是奇函数或是偶函数;
⑤设f(x)与g(x)是定义在R上的两个函数,若对任意x1,x2∈R(x1≠x2)有|f(x1)-f(x2)|>|g(x1)-g(x2)|恒成立,且函数f(x)在R上递增,则函数h(x)=f(x)-g(x)在R上递增.
其中正确的命题是 (写出所有真命题的序号)
【答案】分析:①根据绝对值的性质进行判断;
②根据对称轴的公式进行判断;
③根据抽象函数的定义域的性质进行判断;
④利用函数的绝对值的性质,对其判断;
⑤利用函数的单调性的定义和性质进行判断.
解答:解:①∵函数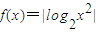 ≥0,显然有最小值,故①错误;
≥0,显然有最小值,故①错误;
②∵函数g(x)=x2-2x-3的对称轴x=1,
因为函数f(x)=|x2-2x-3|与函数g(x)=x2-2x-3对称轴一样,
∴函数f(x)=|x2-2x-3|的图象关于直线x=1对称,故②正确;
③若函数f(x)的定义域为(0,1),
则函数f(x2)的定义域为(-1,0)∪(0,1),故③错误;
④∵|f(-x)|=|f(x)|,
∴f(-x)=f(x)或f(-x)=-f(x),
∴函数f(x)或是奇函数或是偶函数,故④正确;
⑤∵对任意x1,x2∈R(x1≠x2)有|f(x1)-f(x2)|>|g(x1)-g(x2)|恒成立,
且函数f(x)在R上递增,
∴函数h(x)=f(x)-g(x)在R上递增.故⑤正确;
故答案为②④⑤;
点评:此题主要考查二次函数,抽象函数,以及奇偶函数的性质,用定义法判断函数的增减性,知识点比较多比较全面,是一道小型综合题,难度不是很大.
②根据对称轴的公式进行判断;
③根据抽象函数的定义域的性质进行判断;
④利用函数的绝对值的性质,对其判断;
⑤利用函数的单调性的定义和性质进行判断.
解答:解:①∵函数
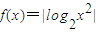 ≥0,显然有最小值,故①错误;
≥0,显然有最小值,故①错误;②∵函数g(x)=x2-2x-3的对称轴x=1,
因为函数f(x)=|x2-2x-3|与函数g(x)=x2-2x-3对称轴一样,
∴函数f(x)=|x2-2x-3|的图象关于直线x=1对称,故②正确;
③若函数f(x)的定义域为(0,1),
则函数f(x2)的定义域为(-1,0)∪(0,1),故③错误;
④∵|f(-x)|=|f(x)|,
∴f(-x)=f(x)或f(-x)=-f(x),
∴函数f(x)或是奇函数或是偶函数,故④正确;
⑤∵对任意x1,x2∈R(x1≠x2)有|f(x1)-f(x2)|>|g(x1)-g(x2)|恒成立,
且函数f(x)在R上递增,
∴函数h(x)=f(x)-g(x)在R上递增.故⑤正确;
故答案为②④⑤;
点评:此题主要考查二次函数,抽象函数,以及奇偶函数的性质,用定义法判断函数的增减性,知识点比较多比较全面,是一道小型综合题,难度不是很大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目