题目内容
在平面直角坐标系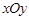 中,圆
中,圆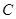 的方程为
的方程为 ,若直线
,若直线 上至少存在一点,使得以该点为圆心,1为半径的圆与圆
上至少存在一点,使得以该点为圆心,1为半径的圆与圆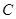 有公共点,则
有公共点,则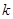 的最大值是 .
的最大值是 .
【答案】
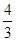
【解析】
试题分析:将圆的方程化简为标准方程,即为由于圆C的方程为(x-4)2+y2=1,由题意可知,直线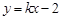 上至少存在一点,使得以该点为圆心,1为半径的圆与圆
上至少存在一点,使得以该点为圆心,1为半径的圆与圆 有公共点,只需(x-4)2+y2=4与直线y=kx-2有公共点即可.
有公共点,只需(x-4)2+y2=4与直线y=kx-2有公共点即可.
∵圆C的方程为x2+y2-8x+15=0,整理得:(x-4)2+y2=1,即圆C是以(4,0)为圆心,1为半径的圆;又直线y=kx-2上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,
∴只需圆C′:(x-4)2+y2=4与直线y=kx-2有公共点即可.设圆心C(4,0)到直线y=kx-2的
距离为d,则d=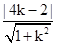 ≤2,即3k2≤4k,∴0≤k≤
≤2,即3k2≤4k,∴0≤k≤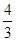 ∴k的最大值是
∴k的最大值是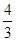
考点:本试题主要考查了直线与圆的位置关系,,考查学生灵活解决问题的能力,属于中档题.
点评:解决该试题的关键是将条件转化为“(x-4)2+y2=4与直线y=kx-2有公共点”。同时能利用点到直线的距离公式得到。

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目