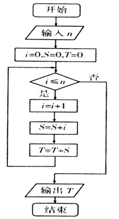
题目内容
设集合A={1,2,3,…8,9}当x∈A时,若有x+1∉A且x-1∉A则称元素x是集合A的一个孤立元.在集合A中任取3个不同的数.
(Ⅰ)求这3个数中恰有1个是奇数的概率;
(Ⅱ)设ξ为这3个数中孤立元的个数(例如:若取出的数为1,2,4,则孤立元为4,此时ξ的值是1),求随机变量ξ的分布列及其数学期望Eξ.
(Ⅰ)求这3个数中恰有1个是奇数的概率;
(Ⅱ)设ξ为这3个数中孤立元的个数(例如:若取出的数为1,2,4,则孤立元为4,此时ξ的值是1),求随机变量ξ的分布列及其数学期望Eξ.
(I)∵集合A={1,2,3,…8,9}共有9个元素
故在集合A中任取3个不同的数共有
种不同情况;
其中恰有1个是奇数有
种不同情况;
故这3个数中恰有1个是奇数的概率P=
=
(II)由孤立元的定义可得
从集合A中任取3个不同的数孤立元可能有0个,1个或3个
即ξ的取值为0,1,3
∵P(ξ=0)=
=
P(ξ=1)=
=
∴P(ξ=3)=1-P(ξ=0)-P(ξ=1)=
∴随机变量ξ的分布列为
则随机变量ξ的数学期望Eξ=0×
+1×
+3×
=
故在集合A中任取3个不同的数共有
| C | 39 |
其中恰有1个是奇数有
| C | 15 |
| C | 24 |
故这3个数中恰有1个是奇数的概率P=
| ||||
|
| 5 |
| 14 |
(II)由孤立元的定义可得
从集合A中任取3个不同的数孤立元可能有0个,1个或3个
即ξ的取值为0,1,3
∵P(ξ=0)=
| 7 | ||
|
| 1 |
| 12 |
P(ξ=1)=
| 42 | ||
|
| 6 |
| 12 |
∴P(ξ=3)=1-P(ξ=0)-P(ξ=1)=
| 5 |
| 12 |
∴随机变量ξ的分布列为
| 0 | 1 | 3 | |||||||
| P |
|
|
|
| 1 |
| 12 |
| 6 |
| 12 |
| 5 |
| 12 |
| 7 |
| 4 |

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目

 、
、 ,记随机变量
,记随机变量 .
. 时的概率;
时的概率; 的概率分布列及数学期望。
的概率分布列及数学期望。