题目内容
在直角坐标系xOy中,椭圆C1: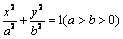 的左、右焦点分别为F1、F2,其中右焦点F2也是拋物线C2:y2 =
4x的焦点,点M为C1与C2在第一象限的交点,且|MF2| =
的左、右焦点分别为F1、F2,其中右焦点F2也是拋物线C2:y2 =
4x的焦点,点M为C1与C2在第一象限的交点,且|MF2| = 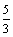 .
.
(1)求椭圆C1的方程;
(2)设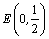 ,是否存在斜率为k (k≠0)的直线l与椭圆C1交于A、B两点,且|AE| = |BE|?若存在,求k的取值范围;若不存在,请说明理由.
,是否存在斜率为k (k≠0)的直线l与椭圆C1交于A、B两点,且|AE| = |BE|?若存在,求k的取值范围;若不存在,请说明理由.
【答案】
【解析】(1)由已知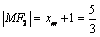
得 代入
代入 得
得 ,即
,即 代入椭圆方程
代入椭圆方程
又 求得
求得 ,故椭圆
,故椭圆 的方程为
的方程为 ……5分
……5分
(2)设直线l的方程为y = kx + m (k≠0),
代入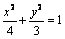
 .
.
 .……8分
.……8分
直线l与椭圆C,有两个不同公共点的充要条件是 (*)
(*)
设AB中点P
(x0,y0),则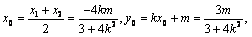
|AE|
= |BE|等价于PE⊥AB,即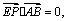
 ……10分
……10分
(1,k)为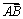 的一个方向向量,故
的一个方向向量,故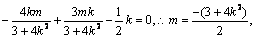 ……11分
……11分
代入(*)得
因此存在合条件的直线l,其斜率k的范围为 …………13分
…………13分

练习册系列答案
相关题目
 如图所示,在直角坐标系xOy中,射线OA在第一象限,且与x轴的正半轴成定角60°,动点P在射线OA上运动,动点Q在y轴的正半轴上运动,△POQ的面积为
如图所示,在直角坐标系xOy中,射线OA在第一象限,且与x轴的正半轴成定角60°,动点P在射线OA上运动,动点Q在y轴的正半轴上运动,△POQ的面积为