题目内容
如果直线l:y=kx-5与圆x2+y2-2x+my-4=0交于M、N两点,且M、N关于直线2x+y=0对称,则直线l被圆截得的弦长为 .
【答案】分析:把圆的方程化为标准式,求出圆心坐标和半径,由题意得,直线l:y=kx-5与直线2x+y=0垂直,圆心(1, )在直线2x+y=0上,求出 k、m,求出圆心到直线l的距离d,由弦长公式求得直线l被圆截得的弦长.
)在直线2x+y=0上,求出 k、m,求出圆心到直线l的距离d,由弦长公式求得直线l被圆截得的弦长.
解答:解:圆x2+y2-2x+my-4=0 即 ,表示圆心为(1,
,表示圆心为(1,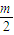 ),
),
半径等于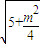 的圆.
的圆.
由题意得,直线l:y=kx-5与直线2x+y=0垂直,∴k•(-2)=-1,∴k= ,
,
∴直线l方程为 x-2y-10=0.
而且圆心(1, )在直线2x+y=0上,∴2+
)在直线2x+y=0上,∴2+ =0,
=0,
∴m=-4,∴圆心(1,-2) 到直线l的距离等于 d=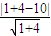 =
=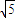 ,
,
故直线l被圆截得的弦长为 2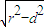 =2
=2 =2
=2 =4.
=4.
故答案为 4.
点评:本题考查直线和圆的位置关系,点到直线的距离公式,弦长公式的应用,判断圆心(1,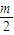 )在直线2x+y=0上,
)在直线2x+y=0上,
求出 m值是解题的难点.
 )在直线2x+y=0上,求出 k、m,求出圆心到直线l的距离d,由弦长公式求得直线l被圆截得的弦长.
)在直线2x+y=0上,求出 k、m,求出圆心到直线l的距离d,由弦长公式求得直线l被圆截得的弦长.解答:解:圆x2+y2-2x+my-4=0 即
 ,表示圆心为(1,
,表示圆心为(1,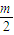 ),
),半径等于
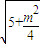 的圆.
的圆. 由题意得,直线l:y=kx-5与直线2x+y=0垂直,∴k•(-2)=-1,∴k=
 ,
,∴直线l方程为 x-2y-10=0.
而且圆心(1,
 )在直线2x+y=0上,∴2+
)在直线2x+y=0上,∴2+ =0,
=0,∴m=-4,∴圆心(1,-2) 到直线l的距离等于 d=
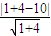 =
=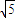 ,
,故直线l被圆截得的弦长为 2
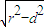 =2
=2 =2
=2 =4.
=4.故答案为 4.
点评:本题考查直线和圆的位置关系,点到直线的距离公式,弦长公式的应用,判断圆心(1,
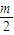 )在直线2x+y=0上,
)在直线2x+y=0上,求出 m值是解题的难点.

练习册系列答案
相关题目