题目内容
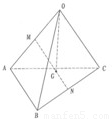
 已知如图,空间四边形OABC,其对角线为OB、AC,M、N分别是对边OA、BC的中点,点G在线段MN上,且使MG=2GN,
已知如图,空间四边形OABC,其对角线为OB、AC,M、N分别是对边OA、BC的中点,点G在线段MN上,且使MG=2GN,| OG |
| OA |
| OB |
| OC |
分析:以
,
,
为一组基向量,首先
=
+
,再将
,
逐步地用基向量表示,最后合并整理得出结果.
| OA |
| OB |
| OC |
| OG |
| OM |
| MG |
| OM |
| MG |
解答:解:
=
+
=
+
=
+
(
-
)
=
+
[
(
+
)-
]
=
+
+
∴x+y+z=
故选B.
| OG |
| OM |
| MG |
| 1 |
| 2 |
| OA |
| 2 |
| 3 |
| MN |
| 1 |
| 2 |
| OA |
| 2 |
| 3 |
| ON |
| OM |
=
| 1 |
| 2 |
| OA |
| 2 |
| 3 |
| 1 |
| 2 |
| OB |
| OC |
| 1 |
| 2 |
| OA |
=
| 1 |
| 6 |
| OA |
| 1 |
| 3 |
| OB |
| 1 |
| 3 |
| OC |
∴x+y+z=
| 5 |
| 6 |
故选B.
点评:本题考查空间向量基本定理,关键是灵活准确的将不是基底中的向量的情况,转化为基向量.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
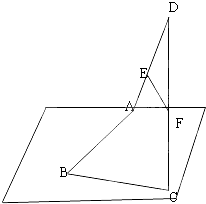 已知:如图,空间四边形ABCD中,E、F分别是DA、DC的中点.求证:EF∥平面ABC.
已知:如图,空间四边形ABCD中,E、F分别是DA、DC的中点.求证:EF∥平面ABC.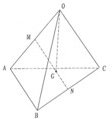 已知如图,空间四边形OABC,其对角线为OB、AC,M、N分别是对边OA、BC的中点,点G在线段MN上,且使MG=2GN,
已知如图,空间四边形OABC,其对角线为OB、AC,M、N分别是对边OA、BC的中点,点G在线段MN上,且使MG=2GN,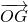 =x
=x +y
+y +z
+z ,则x+y+z=
,则x+y+z=


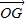 =x
=x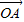 +y
+y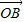 +z
+z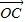 ,则x+y+z=( )
,则x+y+z=( )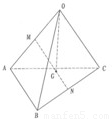



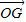 =x
=x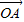 +y
+y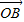 +z
+z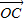 ,则x+y+z=( )
,则x+y+z=( )