题目内容

定义在区间（0，）上的函f(x)满足：（1）f(x)不恒为零；（2）对任何实数x、q,都有.

（1）求证：方程f(x)=0有且只有一个实根；

（2）若a>b>c>1,且a、b、c成等差数列，求证：；

（3）（本小题只理科做）若f(x) 单调递增，且m>n>0时，有，求证：

证明见解析


解析:

(1)取x=1,q=2,有

若存在另一个实根，使得

（2），

，则0，∴，又a+c=2b,

∴ac-b=

即ac<b

(3)

又

令m=b,n=,b且q

则f(m)+f(n)=(qf(b)=f(mn)=0且

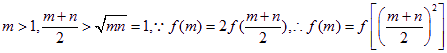
即4m=,由0<n<1得，

练习册系列答案
相关题目
已知定义在区间（0，+∞）上的函数f（x）满足f(
x1x2
)=f(x1)-f(x2)，且当x＞1时f（x）＜0．
（1）求f（1）的值
（2）判断f（x）的单调性
（3）若f（3）=-1，解不等式f（|x|）＜2．
已知定义在区间（0，+∞）上的函数f（x）满足f（
x1x2
）=f（x1）-f（x2），且当x＞1时，f（x）＜0．
①求f（1）的值；
②判断f（x）的单调性；
③若f（3）=-1，解不等式f（|x|）＜-2．
已知定义在区间（0，+∞）上的函数f（x）满足f(
x1x2
)=f(x1)-f(x2)，且当x＞1时，f（x）＜0．
（1）求f（1）的值；
（2）判断f（x）的单调性并予以证明；
（3）若f（3）=-1，解不等式f（log2x）＞-2．
定义在区间（0，+∞）上的函数f（x）满足对任意的实数x，y都有f（xy）=yf（x）
（Ⅰ）求f（1）的值；
（Ⅱ）若f(
1
2
)＜0，求证：f（x）在（0，+∞）上是增函数；
（Ⅲ）若f(
1
2
)＜0，解不等式f（|3x-2|-2x）＜0．
已知定义在区间（0，+∞）上的函数f（x）满足：对?x1，x2∈（0，+∞）恒有f(
x1x2
)=f(x1)-f(x2)，且当x＞1时，f（x）＜0．
（1）求f（1）的值；
（2）证明：函数f（x）在区间（0，+∞）上为单调递减函数；
（3）若f（3）=-1，
（ⅰ）求f（9）的值；（ⅱ）解不等式：f（3x）＜-2．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网