题目内容
(本小题满分12分)
已知函数f(x)=ex+ax-1(e为自然对数的底数).
(Ⅰ)当a=1时,求过点(1,f(1))处的切线与坐标轴围成的三角形的面积;
(II)若f(x)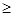 x2在(0,1
)上恒成立,求实数a的取值范围.
x2在(0,1
)上恒成立,求实数a的取值范围.
【答案】
(Ⅰ) ;(II)
;(II)  .
.
【解析】
试题分析:(Ⅰ)利用导数先求过点(1,f(1))处的切线的方程,再求切线与坐标轴的交点坐标,易得三角型面积;(II) 由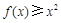 得
得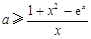 ,令
,令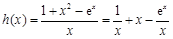 ,利用导数求函数
,利用导数求函数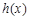 在
在 上的单调性,便可得结论.
上的单调性,便可得结论.
试题解析:(Ⅰ)当 时,
时, ,
,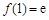 ,
,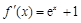 ,
, ,
,
函数 在点
在点 处的切线方程为
处的切线方程为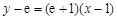 ,即
,即 ,
2分
,
2分
设切线与x、y轴的交点分别为A,B.
令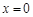 得
得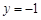 ,令
,令 得
得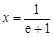 ,∴
,∴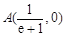 ,
, ,
,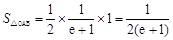 .
.
在点 处的切线与坐标轴围成的图形的面积为
处的切线与坐标轴围成的图形的面积为 . 4分
. 4分
(Ⅱ)由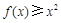 得
得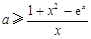 ,
,
令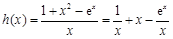 ,
,

令 , 6分
, 6分
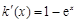 ,∵
,∵ ,∴
,∴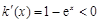 ,
, 在
在 为减函数,
为减函数,
∴ ,
8分
,
8分
又∵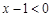 ,
,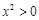 ∴
∴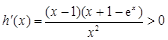 ∴
∴ 在
在 为增函数, 10分
为增函数, 10分
 ,因此只需
,因此只需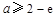 .
12分
.
12分
考点:1、利用导数求切线方程;2、利用导数求函数的单调性;3、导数运算与函数的综合运用.

练习册系列答案
相关题目