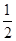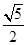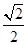题目内容
已知函数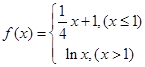 则方程
则方程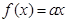 恰有两个不同的实根时,实数a的取值范围是(注:e为自然对数的底数)( )
恰有两个不同的实根时,实数a的取值范围是(注:e为自然对数的底数)( )
A.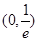 | B. | C.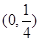 | D.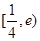 |
B
解析试题分析:∵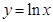 ,∴
,∴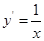 ,设切点为
,设切点为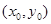 ,∴切线方程为
,∴切线方程为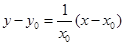 ,
,
∴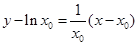 ,与
,与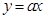 相同,∴
相同,∴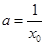 ,
,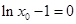 ,∴
,∴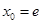 ,∴
,∴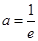 .
.
当直线与 平行时,直线为
平行时,直线为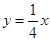 ,
,
当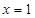 时,
时,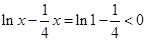 ,
,
当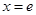 时,
时,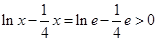 ,
,
当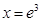 时,
时,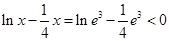 ,所以
,所以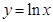 与
与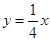 在
在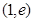 ,
,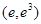 上有2个交点,所以直线在
上有2个交点,所以直线在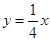 和
和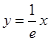 之间时与函数
之间时与函数 有2个交点,所以
有2个交点,所以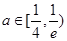 ,故选B.
,故选B.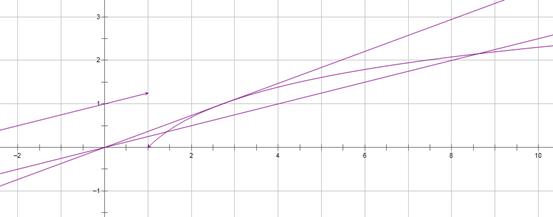
考点:1.导数的运算;2.利用导数求曲线的切线;3.函数图像的交点.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
函数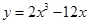 在区间
在区间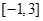 上的最大值和最小值分别为
上的最大值和最小值分别为
A.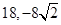 | B.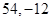 | C.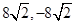 | D.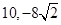 |
设函数
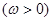 的导数
的导数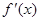 的最大值为3,则
的最大值为3,则 的图象的一条对称轴的方程是
的图象的一条对称轴的方程是
A.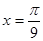 | B. | C.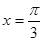 | D.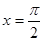 |
若函数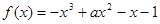 在
在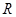 上是单调函数,则实数
上是单调函数,则实数 的取值范围是( )
的取值范围是( )
A.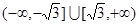 | B.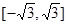 |
C.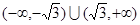 | D.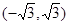 |
若实数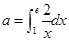 ,则函数
,则函数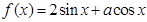 的图象的一条对称轴方程为( )
的图象的一条对称轴方程为( )
A.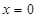 | B. | C.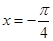 | D.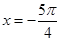 |
函数f(x)的图象如图所示,下列数值排序正确的是( ).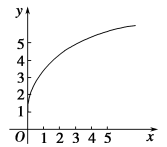
| A.0<f′(2)<f′(3)<f(3)-f(2) |
| B.0<f′(3)<f(3)-f(2)<f′(2) |
| C.0<f(3)<f′(2)<f(3)-f(2) |
| D.0<f(3)-f(2)<f′(2)<f′(3) |
已知f(x)=x3+ax2+(a+6)x+1有极大值和极小值,则a的取值范围为( ).
| A.-1<a<2 | B.-3<a<6 |
| C.a<-1或a>2 | D.a<-3或a>6 |
直线y=a与函数y=x3-3x的图象有三个相异的交点,则a的取值范围为 ( ).
| A.(-2,2) | B.[-2,2] |
| C.[2,+∞) | D.(-∞,-2] |