题目内容
【题目】已知函数f(x)=|x+2|+|x+a|(a∈R).
(Ⅰ)若a=5,求函数f(x)的最小值,并写出此时x的取值集合;
(Ⅱ)若f(x)≥3恒成立,求a的取值范围.
【答案】解:(Ⅰ)若a=5,f(x)=|x+2|+|x+5|= 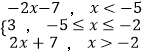 .
.
其图象如图: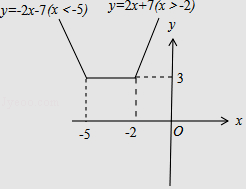
∴f(x)的最小值为3,使f(x)取得最小值的x的集合为{x|﹣5≤x≤﹣2};
(Ⅱ)f(x)=|x+2|+|x+a|=|x﹣(﹣2)|+|x﹣(﹣a)|,
由绝对值的几何意义可知,f(x)为数轴上动点x与两个定点﹣2、﹣a的距离的和,
如图:![]()
当动点x与﹣2重合时,|x﹣(﹣2)|最小为0,要使f(x)≥3恒成立,
则|﹣2﹣(﹣a)|≥3,即|a﹣2|≥3,得a﹣2≤﹣3或a﹣2≥3,
∴a≤﹣1或a≥5
【解析】(Ⅰ)写出分段函数,画图得答案;(Ⅱ)由绝对值的几何意义,把f(x)≥3恒成立转化为关于a的含有绝对值的不等式求解.

练习册系列答案
相关题目
