题目内容
若正四棱柱 的底面边长为2,高为4,则异面直线
的底面边长为2,高为4,则异面直线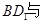
 所成角的正切值是_________________.
所成角的正切值是_________________.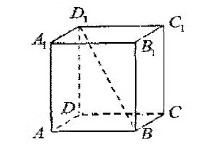

解析试题分析:根据正四棱柱的几何特征,我们易根据AD∥BC,得到∠D1BC即为异面直线BD1与AD所成角,根据已知中正四棱柱ABCD-A1B1C1D1的底面边长为2,高为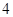 ,求出△D1BC中各边的长,解△D1BC即可得到答案.
,求出△D1BC中各边的长,解△D1BC即可得到答案.
∵AD∥BC∴∠D1BC即为异面直线BD1与AD所成角连接D1C,在△D1BC中,∵正四棱柱ABCD-A1B1C1D1的底面边长为2,高为4∴D1B=2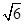 ,BC=2,D1C=
,BC=2,D1C=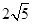 ∴cos∠D1BC=
∴cos∠D1BC=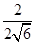 ,故异面直线BD1与AD所成角的正切值为
,故异面直线BD1与AD所成角的正切值为
故答案为 。
。
考点:本题主要是考查查的知识点是异面直线及其所成的角。
点评:解决该试题的关键是根据已知条件确定找到两条异面直线夹角,易根据AD∥BC,得到∠D1BC即为异面直线BD1与AD所成角

练习册系列答案
 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
 平面ABC,
平面ABC, ,给出下列结论:①
,给出下列结论:① ;②平面
;②平面 平面PBC;③直线
平面PBC;③直线 平面PAE;④
平面PAE;④ ;⑤直线PD与平面PAB所成角的余弦值为
;⑤直线PD与平面PAB所成角的余弦值为 。
。
 、
、 ,直线
,直线 ,若
,若 ,
, ,则
,则 ;④四个侧面两两全等的四棱柱为直四棱柱;⑤底面是等边三角形,侧面都是等腰三角形的三棱锥是正三棱锥.其中正确命题的序号是 .
;④四个侧面两两全等的四棱柱为直四棱柱;⑤底面是等边三角形,侧面都是等腰三角形的三棱锥是正三棱锥.其中正确命题的序号是 .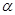 ,其中m∥n,那么在平面
,其中m∥n,那么在平面 、
、 ,两个不同平面
,两个不同平面 、
、 ,给出下列命题:
,给出下列命题:
 ,则
,则 的面对角线
的面对角线 上运动,则下列四个命题:①三棱锥
上运动,则下列四个命题:①三棱锥 的体积不变; ②
的体积不变; ② ∥面
∥面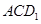 ; ③
; ③ ; ④面
; ④面 面
面
