题目内容
(本小题满分12分)
已知椭圆C: 的短轴长为
的短轴长为 ,且斜率为
,且斜率为 的直线
的直线 过椭圆C的焦点及点
过椭圆C的焦点及点 。
。
(Ⅰ)求椭圆C的方程;
(Ⅱ)已知一直线 过椭圆C的左焦点
过椭圆C的左焦点 ,交椭圆于点P、Q,
,交椭圆于点P、Q,
(ⅰ)若满足 (
( 为坐标原点),求
为坐标原点),求 的面积;
的面积;
(ⅱ)若直线 与两坐标轴都不垂直,点M在
与两坐标轴都不垂直,点M在 轴上,且使
轴上,且使 为
为 的一条角平分线,则称点M为椭圆C的“左特征点”,求椭圆C的左特征点。
的一条角平分线,则称点M为椭圆C的“左特征点”,求椭圆C的左特征点。
【答案】
(Ⅰ)椭圆C的方程为 ;
;
(Ⅱ)(ⅰ)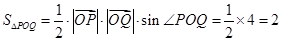 ,
,
(ⅱ)椭圆C的左特征点为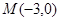 .
.
【解析】本试题主要是考查了椭圆方程的求解以及直线与椭圆的位置关系的运用,三角形面积的求解的综合运用。
(1)由题意可知,直线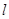 的方程为
的方程为 ,………………………1分
,………………………1分
∵直线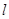 过椭圆C的焦点,∴该焦点坐标为
过椭圆C的焦点,∴该焦点坐标为 ∴
∴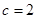 ,
,
结合短轴长,得到a,b,c的值,得到椭圆的方程。
(2)因为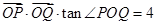 ,借助于正弦面积公式求解得到结论。
,借助于正弦面积公式求解得到结论。
(3)设直线PQ的方程为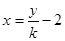 ,直线与椭圆联立方程组,借助于
,直线与椭圆联立方程组,借助于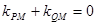 得到参数的关系式,进而得到特征点。
得到参数的关系式,进而得到特征点。
解:(Ⅰ)由题意可知,直线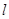 的方程为
的方程为 ,………………………1分
,………………………1分
∵直线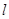 过椭圆C的焦点,∴该焦点坐标为
过椭圆C的焦点,∴该焦点坐标为 ∴
∴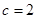 ,
,
又椭圆C的短轴长为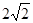 ,∴
,∴ ,∴
,∴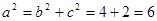 ,
,
∴椭圆C的方程为 ;…………………………………………………………3分
;…………………………………………………………3分
(Ⅱ)(ⅰ)∵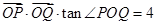 ,
,
∴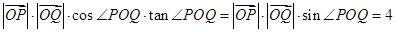 ,……………5分
,……………5分
∴ ,……………………………6分
,……………………………6分
(ⅱ)设左特征点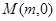 ,左焦点为
,左焦点为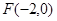 ,可设直线PQ的方程为
,可设直线PQ的方程为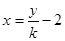 ,
,
由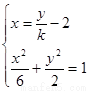 消去
消去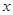 得
得 ,
,
设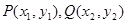 则
则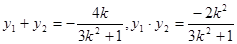 ,…………………8分
,…………………8分
∵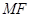 为
为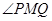 的一条角平分线,
的一条角平分线,
∴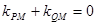 ,即
,即 ,………………………………………9分
,………………………………………9分
又 ,
, ,代入上式可得
,代入上式可得
∴ ,
,
解得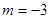 ,……………………………………………………………………………11分
,……………………………………………………………………………11分
∴椭圆C的左特征点为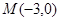 .………………………………………………………12分
.………………………………………………………12分

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目