题目内容
【题目】已知函数![]() 的图像与
的图像与![]() 轴相切,
轴相切,![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,求证:
,求证:![]() .
.
【答案】(1)证明见解析;(2)证明见解析
【解析】
(1)求出![]() 的导数,设
的导数,设![]() 的图象与x轴相交于点
的图象与x轴相交于点![]() ,可得
,可得 ,解方程可得
,解方程可得![]() ,原不等式等价于
,原不等式等价于![]() ,设
,设![]() ,求出导数和单调区间,可得极值、最值,即可得证;
,求出导数和单调区间,可得极值、最值,即可得证;
(2)设![]() ,求出导数,运用(1)的结论可得
,求出导数,运用(1)的结论可得![]() 单调递增,再由不等式的性质可得
单调递增,再由不等式的性质可得![]() ,即
,即![]() ,再运用
,再运用![]() 的单调性和不等式的性质,证得
的单调性和不等式的性质,证得![]() ,进而证得右边不等式.
,进而证得右边不等式.
(1)由题得![]() ,设
,设![]() 的图像与
的图像与![]() 轴相切于点
轴相切于点![]() ,则
,则
 ,即
,即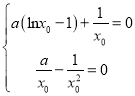 ,解得
,解得![]() ,
,
所以![]() ,则
,则![]() ,即为
,即为![]() .
.
设![]() ,则
,则![]() .
.
当![]() 时,
时,![]() ,
,![]() 单调递增;当
单调递增;当![]() 时,
时,![]() ,
,![]() 单调递减.
单调递减.
所以![]() ,即
,即![]() ,
,
所以![]() ;
;
(2)先证![]() ,设
,设![]() ,则
,则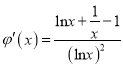 ,
,
由(1)可知,当![]() 时,
时,![]() ,从而有
,从而有![]() ,所以
,所以![]() 单调递增.
单调递增.
又![]() ,从而有
,从而有![]() ,即
,即![]() ,
,
所以![]() ,即
,即![]() .
.
再证![]() ,因为
,因为![]()
![]() ,
,
又由(1)知,![]() ,故
,故![]() 在
在![]() 单调递增,
单调递增,
则![]() ,即
,即![]() ,所以
,所以![]() .
.
又![]() ,所以
,所以![]() .
.
综上可知,![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】《流浪地球》是由刘慈欣的科幻小说改编的电影,在2019年春节档上影,该片上影标志着中国电影科幻元年的到来;为了振救地球,延续百代子孙生存的希望,无数的人前仆后继,奋不顾身的精神激荡人心,催人奋进.某网络调查机构调查了大量观众的评分,得到如下统计表:
评分 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
频率 | 0.03 | 0.02 | 0.02 | 0.03 | 0.04 | 0.05 | 0.08 | 0.15 | 0.21 | 0.36 |
(1)求观众评分的平均数?
(2)视频率为概率,若在评分大于等于8分的观众中随机地抽取1人,他的评分恰好是10分的概率是多少?
(3)视频率为概率,在评分大于等于8分的观众中随机地抽取4人,用![]() 表示评分为10分的人数,求
表示评分为10分的人数,求![]() 的分布列及数学期望.
的分布列及数学期望.
