题目内容
(2013•青岛二模)已知函数f(x)=sin(2x+
)-2cos2x.
(Ⅰ)求函数f(x)在[0,π]上的单调递增区间;
(Ⅱ)设△ABC的内角A,B,C的对应边分别为a,b,c,且f(A)=0,若向量
=(1,sinB)与向量
=(2,sinC)共线,求
的值.
| π |
| 6 |
(Ⅰ)求函数f(x)在[0,π]上的单调递增区间;
(Ⅱ)设△ABC的内角A,B,C的对应边分别为a,b,c,且f(A)=0,若向量
| m |
| n |
| a |
| b |
分析:(Ⅰ)利用三角函数的恒等变换化简函数f(x)的解析式为sin(2x-
)-1.令2kπ-
≤2x-
≤2kπ+
(k∈Z),求得x的范围,即可得到函数的单调递增区间,从而求得函数f(x)在[0,π]上的单调递增区间.
(Ⅱ)由f(A)=sin(2A-
)-1=0,求得A的值.由向量
=(1,sinB)与向量
=(2,sinC)共线,可得sinC=2sinB,由正弦定理得c=2b,再由余弦定理求得
的值.
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
(Ⅱ)由f(A)=sin(2A-
| π |
| 6 |
| m |
| n |
| a |
| b |
解答:解:(Ⅰ)f(x)=sin(2x+
)-2cos2x=sin2xcos
+cos2xsin
-(cos2x+1)=
sin2x-
cos2x-1=sin(2x-
)-1,…(3分)
由2kπ-
≤2x-
≤2kπ+
(k∈Z) 求得:kπ-
≤x≤kπ+
(k∈Z),
所以,f(x)在[0,π]上的单调递增区间为[0,
],[
,π].…(6分)
(Ⅱ)∵f(A)=sin(2A-
)-1=0,则sin(2A-
)=1.
∵0<A<π,∴-
<2A-
<
,∴2A-
=
,A=
.…(8分)
∵向量
=(1,sinB)与向量
=(2,sinC)共线,
∴sinC=2sinB,由正弦定理得,c=2b.…(10分)
由余弦定理得,a2=b2+c2-2bccos
,即a2=b2+4b2-2b2,
解得
=
…(12分)
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| ||
| 2 |
| 1 |
| 2 |
| π |
| 6 |
由2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 3 |
所以,f(x)在[0,π]上的单调递增区间为[0,
| π |
| 3 |
| 5π |
| 6 |
(Ⅱ)∵f(A)=sin(2A-
| π |
| 6 |
| π |
| 6 |
∵0<A<π,∴-
| π |
| 6 |
| π |
| 6 |
| 11π |
| 6 |
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
∵向量
| m |
| n |
∴sinC=2sinB,由正弦定理得,c=2b.…(10分)
由余弦定理得,a2=b2+c2-2bccos
| π |
| 3 |
解得
| a |
| b |
| 3 |
点评:本题主要考查三角函数的恒等变换及化简求值,正弦函数的单调性,正弦定理、余弦定理、以及两个向量共线的性质,属于中档题.

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
 (2013•青岛二模)一同学为研究函数f(x)=
(2013•青岛二模)一同学为研究函数f(x)=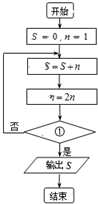 (2013•青岛二模)执行如图所示的程序框图.若输出S=31,则框图中①处可以填入( )
(2013•青岛二模)执行如图所示的程序框图.若输出S=31,则框图中①处可以填入( )