题目内容
已知△ABC是边长为1的正三角形，点D、E分别是边AB、AC上的点，线段DE经过△ABC的中心G，
=p
，
=q
（0＜m≤1，0＜n≤1）则
+
等于（ ）
| AD |
| AB |
| AE |
| AC |
| 1 |
| p |
| 1 |
| q |
| A、3 | B、2 | C、1.5 | D、1 |
分析：充分运用向量的几何形式运算及向量平行的定理及推论，把相关向量用已知向量表示即可
解答：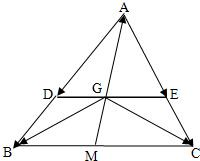
解：
=
(
+
).因为G是△ABC的重心，
所以
=
=
•(
+
)；由D、G、E三点共线，有
，
共线，
所以，有且只有一个实数λ，
=λ
.
而
=
-
=
(
+
)-p
=(
-p)
+
=
-
=q
-
(
+
)=-
+(q-
)
，
所以(
-p)
+
=λ[-
+(q-
)
]．
又因为
、
不共线，所以
，消去λ，整理得3pq=p+q，故
+
=3，
故选A．
解：| AM |
| 1 |
| 2 |
| AB |
| AC |
所以
| AG |
| 2 |
| 3 |
| AM |
| 1 |
| 3 |
| AB |
| AC |
| DG |
| GE |
所以，有且只有一个实数λ，
| DG |
| GE |
而
| DG |
| AG |
| AD |
| 1 |
| 3 |
| AB |
| AC |
| AB |
| 1 |
| 3 |
| AB |
| 1 |
| 3 |
| AC， |
| GE |
| AE |
| AG |
| AC |
| 1 |
| 3 |
| AB |
| AC |
| 1 |
| 3 |
| AB |
| 1 |
| 3 |
| AC |
所以(
| 1 |
| 3 |
| AB |
| 1 |
| 3 |
| AC |
| 1 |
| 3 |
| AB |
| 1 |
| 3 |
| AC |
又因为
| AB |
| AC |
|
| 1 |
| p |
| 1 |
| q |
故选A．
点评：建立p与q的关系关键是由D，G，E三点共线得出．为此要熟练运用已知向量表示未知向量，平面向量是高中数学中最基本、最常用、最常考的知识之一，注意平面向量与其他知识的联系．
练习册系列答案
阅读快车系列答案
相关题目