Question

写出下列函数的单调区间：①y=-x²+2|x|+1；②y=|-x²+2x+3|．

Answer 1

【答案】分析：分别将两个函数表示为分段函数形式，然后利用二次函数的表达式求出函数的单调区间．
解答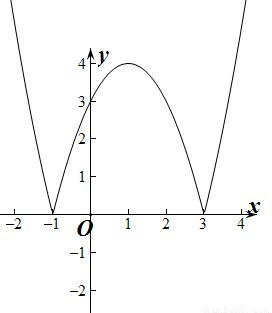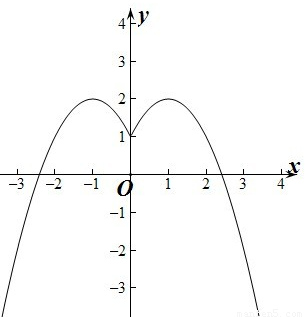：解：①当x≥0时，y=-x²+2|x|+1=y=-x²+2x+1=-（x-1）²+2，
此时函数在[0，1]单调递增，在[1，+∞）是上单调递减．
当x＜0时，y=-x²+2|x|+1=y=-x²-2x+1=-（x+1）²+2，
此时函数在[-1，0）单调递减，在（-∞，-1）是上单调递增．
所以函数的增区间为[0，1]和（-∞，-1）．函数的减区间为[-1，0）和[1，+∞）．
②y=|-x²+2x+3|=|x²-2x-3|，
当x²-2x-3≥0，即x≥3或x≤-1，
此时y=|-x²+2x+3|=|x²-2x-3|=x²-2x-3，
当x∈[3，+∞）时，函数单调递增．当x∈（-∞，-1]时，函数单调递减．
当x²-2x-3＜0，即-1＜x＜3，此时y=|-x²+2x+3|=|x²-2x-3|=-x²+2x+3=-（x-1）²+4，
所以此时函数在（-1，1]上单调递增，在[1，3）上单调递减．
所以函数的增区间为[3，+∞）和（-1，1]．函数的减区间为（-∞，-1]和[1，3）．
点评：本题主要考查二次函数的图象和性质，要求熟练掌握二次函数的图象．