题目内容
已知复数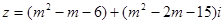 ,
,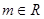
(1)当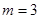 时,求
时,求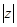 ;
;
(2)当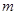 为何值时,
为何值时,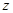 为纯虚数;
为纯虚数;
(3)若复数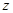 在复平面上所对应的点在第四象限,求实数
在复平面上所对应的点在第四象限,求实数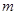 的取值范围。
的取值范围。
(1)利用参数的值,代入根据模的定义来求解。
(2)根据复数的概念来保证实部为零,虚部不为零来求解得到。
(3) 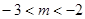 或
或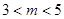
解析试题分析:解:(1)当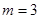 时,
时,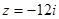 ,所以
,所以 ………2分
………2分
(2)若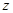 为纯虚数,则
为纯虚数,则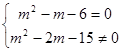 即
即 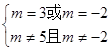 ………6分
………6分
解得: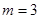 ………7分
………7分
(3)若复数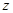 在复平面上所对应的点在第四象限,
在复平面上所对应的点在第四象限,
则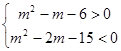 解得:
解得: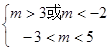 10分
10分
解得: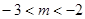 或
或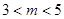 12分
12分
考点:复数的概念和几何意义
点评:解决的关键是熟练的掌握复数的概念和几何意义的理解,属于基础题。

练习册系列答案
相关题目
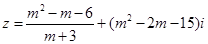
 ,问:当
,问:当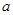 为何实数时?
为何实数时?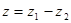 为虚数; (2)
为虚数; (2)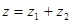 在复平面内对应的点在虚轴的负半轴上;
在复平面内对应的点在虚轴的负半轴上;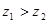
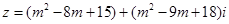 ,实数
,实数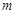 取什么值时,
取什么值时,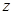 是实数; (2复数
是实数; (2复数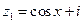 ,
,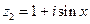 (
(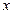
 为实数且
为实数且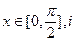 是虚数单位),求函数
是虚数单位),求函数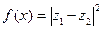 的值域。
的值域。 且复数z=(2+
且复数z=(2+ )
)

 什么值时,复数z是纯虚数;
什么值时,复数z是纯虚数; 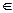 R),已知A={z||z-z1|≤1},B={z||z-z2|≤2},A∩B=φ,求a的取值范围
R),已知A={z||z-z1|≤1},B={z||z-z2|≤2},A∩B=φ,求a的取值范围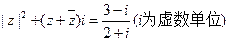 的复数z。
的复数z。