题目内容
已知a为实数,函数f(x)=(x2+1)(x+a),若f′(-1)=0,求函数y=f(x)在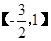 上的最大值和最小值.
上的最大值和最小值.
f(x)在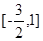 上的最大值为f(1)=6,最小值为f
上的最大值为f(1)=6,最小值为f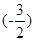 =
=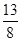
解析试题分析:解: f′(x)=3x2+2ax+1. ..1分
∵f′(-1)=0,∴3-2a+1=0,即a=2 1分
∴f′(x)=3x2+4x+1=3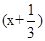 (x+1).
(x+1).
由f′(x)≥0,得x≤-1或x≥-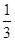 ;由f′(x)≤0,得-1≤x≤-
;由f′(x)≤0,得-1≤x≤-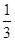
因此,函数f(x)的单调递增区间为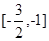 和
和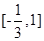 ,
,
单调递减区间为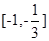 4分
4分
∴f(x)在x=-1取得极大值f(-1)=2,
f(x)在x=-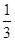 取得极小值f
取得极小值f =
=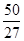 .
.
又∵f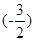 =
=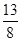 ,f(1)=6,且
,f(1)=6,且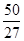 >
>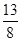 ,
,
∴f(x)在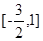 上的最大值为f(1)=6,最小值为f
上的最大值为f(1)=6,最小值为f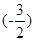 =
=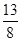 4分
4分
考点:导数的运用
点评:主要是考查了函数的单调性的判定和求解最值的运用,属于基础题。

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
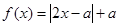 。
。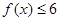 的解集为
的解集为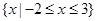 ,求实数
,求实数 的值;
的值;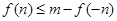 成立,求实数m的取值范围。
成立,求实数m的取值范围。 (
(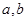
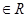 )
)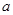 从集合
从集合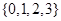 中任取一个元素,
中任取一个元素,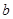 从集合
从集合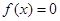 恰有两个不相等实根的概率;
恰有两个不相等实根的概率;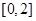 中任取一个数,
中任取一个数,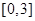 中任取一个数,求方程
中任取一个数,求方程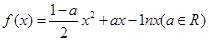 。
。 的极值;
的极值;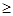 2时,讨论函数
2时,讨论函数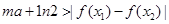 成立,求
成立,求
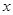 的不等式
的不等式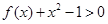
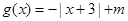 ,
,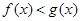 的解集非空,求实数m的取值范围
的解集非空,求实数m的取值范围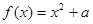 .
.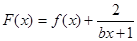 是偶函数,在定义域上
是偶函数,在定义域上 恒成立,求实数
恒成立,求实数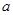 的取值范围;
的取值范围;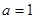 时,令
时,令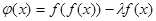 ,问是否存在实数
,问是否存在实数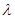 ,使
,使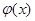 在
在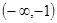 上是减函数,在
上是减函数,在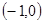 上是增函数?如果存在,求出
上是增函数?如果存在,求出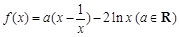 .
.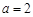 ,求曲线
,求曲线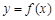 在点
在点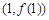 处的切线方程;
处的切线方程;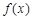 的单调区间;
的单调区间;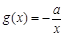 .若至少存在一个
.若至少存在一个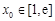 ,使得
,使得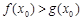 成立,求实数
成立,求实数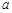 的取值范围.
的取值范围.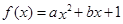 在
在 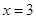 处的切线方程为
处的切线方程为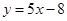 .
.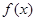 的解析式;
的解析式;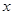 的方程
的方程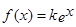 恰有两个不同的实根,求实数
恰有两个不同的实根,求实数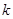 的值 ;
的值 ;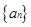 满足
满足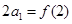 ,
,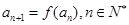 ,求
,求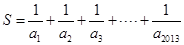 的整数部分.
的整数部分. 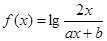 且
且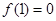 ,当
,当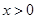 时,恒有
时,恒有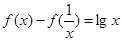
 的解析式;
的解析式;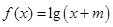 的解集为空集,求
的解集为空集,求 的范围。
的范围。