��Ŀ����
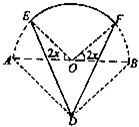 ��ͼ��ʵ�߲���DE��DF��EF��ij�羰����Ƶ��ο۹�·��ƽ��ͼ���������߲���EF����ABΪֱ���İ�Բ�ϵ�һ�λ�����OΪԲ�ģ���ABD����ABΪб�ߵĵ���ֱ�������Σ�����AB=2ǧ�ף���EOA=��FOB=2x(0��x��
��ͼ��ʵ�߲���DE��DF��EF��ij�羰����Ƶ��ο۹�·��ƽ��ͼ���������߲���EF����ABΪֱ���İ�Բ�ϵ�һ�λ�����OΪԲ�ģ���ABD����ABΪб�ߵĵ���ֱ�������Σ�����AB=2ǧ�ף���EOA=��FOB=2x(0��x��| �� | 4 |
��I���Խ�y��ʾΪx�ĺ�����
��II����ȷ����xȡ��ֵʱ���÷羰������ġ������ȡ���ѣ�
�����������ɻ�����ʽ�����AE��BF�ij��ȣ���Բ���ܳ���ʽ�����Բ�ij��ȣ���EF�ij��ȿ�������OD����������ODE��������ODF�У��������Ҷ�������DE��DF�ij��ȣ�Ȼ������ο���ÿ��·���������ġ������ȡ�������Ӧ���߶λij��ȳ����ȣ��ҡ������ȡ���·��DE��DF�ij��ȵı���ϵ��Ϊ2����·��EF�ij��ȵı���ϵ��Ϊ1���÷羰������ġ������ȡ�y���ο���������·�ߡ������ȡ��ĺͽ�y��ʾΪx�ĺ�����
������������к����ĵ��������������������㣬�����Ѷ�����ֶΣ����ݵ������ķ����ж�ԭ�����ڸ����ڵĵ����ԣ��Ӷ��õ���ֵ�㣬ȷ������xȡ��ֵʱ���÷羰������ġ������ȡ���ѣ�
������������к����ĵ��������������������㣬�����Ѷ�����ֶΣ����ݵ������ķ����ж�ԭ�����ڸ����ڵĵ����ԣ��Ӷ��õ���ֵ�㣬ȷ������xȡ��ֵʱ���÷羰������ġ������ȡ���ѣ�
����⣺������ΪOA=
AB=1����EOA=��FOB=2x�����Ի�AE���ڻ�BF�ij�����2x��
�ְ�Բ�ܳ�Ϊ�У����Ի�EF�ij�Ϊ��-4x������OD������OD=OE=OF=1����FOD=��EOD=
+2x��
����DE=DF=
=
=
(sinx+cosx)��
����Ϊ��ÿ��·���������ġ������ȡ�������Ӧ���߶λij��ȳ����ȣ��ҡ������ȡ���·��DE��DF�ij��ȵı���ϵ��Ϊ2����·��EF�ij��ȵı���ϵ��Ϊ1��
���ԣ�y=4
(sinx+cosx)+��-4x ��0��x��
����
������y=4
(sinx+cosx)+��-4x ��0��x��
����
�ã�y��=4
(cosx-sinx)-4��
��y��=0���ã�4
(cosx-sinx)-4=0��
����cos(x+
)=
�����x=
��
�ֵ�x��(0��
)ʱ��y����0�����Դ�ʱy��(0��
)�ϵ���������
��x��(
��
)ʱ��y����0�����Դ�ʱy��(
��
)�ϵ����ݼ���
�ʵ�x=
ʱ������y�����ֵ��
�𣺵�x=
ʱ���÷羰������ġ������ȡ���ѣ�
| 1 |
| 2 |
�ְ�Բ�ܳ�Ϊ�У����Ի�EF�ij�Ϊ��-4x������OD������OD=OE=OF=1����FOD=��EOD=
| �� |
| 2 |
����DE=DF=
1+1-2cos(2x+
|
| 2+2sin2x |
| 2 |
����Ϊ��ÿ��·���������ġ������ȡ�������Ӧ���߶λij��ȳ����ȣ��ҡ������ȡ���·��DE��DF�ij��ȵı���ϵ��Ϊ2����·��EF�ij��ȵı���ϵ��Ϊ1��
���ԣ�y=4
| 2 |
| �� |
| 4 |
������y=4
| 2 |
| �� |
| 4 |
�ã�y��=4
| 2 |
��y��=0���ã�4
| 2 |
����cos(x+
| �� |
| 4 |
| 1 |
| 2 |
| �� |
| 12 |
�ֵ�x��(0��
| �� |
| 12 |
| �� |
| 12 |
��x��(
| �� |
| 12 |
| �� |
| 4 |
| �� |
| 12 |
| �� |
| 4 |
�ʵ�x=
| �� |
| 12 |
�𣺵�x=
| �� |
| 12 |
������������һ����ѧ��ģ���⣬���Ĺؼ��Ƕ������⣬��ȷ�г���������ʽ��Ȼ�����õ��������ڿ������ڵļ�ֵ����һ���õ������ڱ������ڵ���ֵ���������е��⣮

��ϰ��ϵ�д�
�����Ŀ
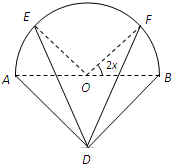 ij��湫˾Ϊ2010���Ϻ������������һ����ƣ���ʽ��ͼ��ʵ�߲�����ʾ�����ϲ�������ABΪֱ���İ�Բ����OΪԲ�ģ��²�������ABΪб�ߵĵ���ֱ�������Σ�DE��DF������֧�ˣ�����AB=2�ף���EOA=��FOB=2x��0��x��
ij��湫˾Ϊ2010���Ϻ������������һ����ƣ���ʽ��ͼ��ʵ�߲�����ʾ�����ϲ�������ABΪֱ���İ�Բ����OΪԲ�ģ��²�������ABΪб�ߵĵ���ֱ�������Σ�DE��DF������֧�ˣ�����AB=2�ף���EOA=��FOB=2x��0��x��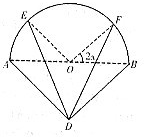 ��ͼ��ʵ�߲�����ij����Ƶ��ο۹�·��ƽ��ͼ�����߲�������ABΪֱ���İ�Բ����OΪԲ�ģ���ABD����ABΪб�ߵĵ���ֱ�������Σ�����AB=2ǧ�ף�
��ͼ��ʵ�߲�����ij����Ƶ��ο۹�·��ƽ��ͼ�����߲�������ABΪֱ���İ�Բ����OΪԲ�ģ���ABD����ABΪб�ߵĵ���ֱ�������Σ�����AB=2ǧ�ף�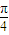 �������ڻ�EF���߶�DE���߶�DF��װ�ʵƣ��ڻ�AE����BF���߶�AD���߶�BD��װ���ܵƣ���ÿ�ֵƵġ�����Ч����������Ӧ���߶λij��ȳ����ȣ��ҲʵƵı���ϵ��Ϊ2k�����ܵƵı���ϵ��Ϊk��k��0�����ٶ����������ġ�����Ч����y�����еơ�����Ч�����ĺͣ�
�������ڻ�EF���߶�DE���߶�DF��װ�ʵƣ��ڻ�AE����BF���߶�AD���߶�BD��װ���ܵƣ���ÿ�ֵƵġ�����Ч����������Ӧ���߶λij��ȳ����ȣ��ҲʵƵı���ϵ��Ϊ2k�����ܵƵı���ϵ��Ϊk��k��0�����ٶ����������ġ�����Ч����y�����еơ�����Ч�����ĺͣ�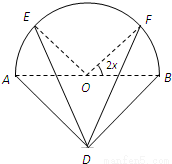
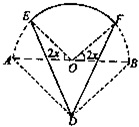 ��ͼ��ʵ�߲���DE��DF��EF��ij�羰����Ƶ��ο۹�·��ƽ��ͼ���������߲���EF����ABΪֱ���İ�Բ�ϵ�һ�λ�����OΪԲ�ģ���ABD����ABΪб�ߵĵ���ֱ�������Σ�����AB=2ǧ�ף�
��ͼ��ʵ�߲���DE��DF��EF��ij�羰����Ƶ��ο۹�·��ƽ��ͼ���������߲���EF����ABΪֱ���İ�Բ�ϵ�һ�λ�����OΪԲ�ģ���ABD����ABΪб�ߵĵ���ֱ�������Σ�����AB=2ǧ�ף�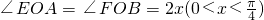 �����ο���ÿ��·���������ġ������ȡ�������Ӧ���߶λij��ȳ����ȣ��ҡ������ȡ���·��DE��DF�ij��ȵı���ϵ��Ϊ2����·��EF�ij��ȵı���ϵ��Ϊ1���ٶ��÷羰������ġ������ȡ�y���ο���������·�ߡ������ȡ��ĺͣ�
�����ο���ÿ��·���������ġ������ȡ�������Ӧ���߶λij��ȳ����ȣ��ҡ������ȡ���·��DE��DF�ij��ȵı���ϵ��Ϊ2����·��EF�ij��ȵı���ϵ��Ϊ1���ٶ��÷羰������ġ������ȡ�y���ο���������·�ߡ������ȡ��ĺͣ�