题目内容
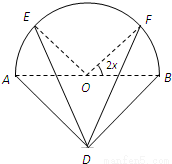
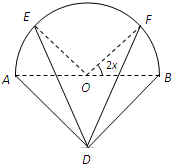 某广告公司为2010年上海世博会设计了一种霓虹灯,样式如图中实线部分所示.其上部分是以AB为直径的半圆,点O为圆心,下部分是以AB为斜边的等腰直角三角形,DE,DF是两根支杆,其中AB=2米,∠EOA=∠FOB=2x(0<x<
某广告公司为2010年上海世博会设计了一种霓虹灯,样式如图中实线部分所示.其上部分是以AB为直径的半圆,点O为圆心,下部分是以AB为斜边的等腰直角三角形,DE,DF是两根支杆,其中AB=2米,∠EOA=∠FOB=2x(0<x<| π | 4 |
(1)试将y表示为x的函数;
(2)试确定当x取何值时,该霓虹灯整体的“心悦效果”最佳.
分析:(1)由题意知,建立三角函数模型,根据所给的条件看出要用的三角形的边长和角度,用余弦定理写出要求的边长,表述出函数式,整理变化成最简的形式,得到结果.
(2)要求函数的单调性,对上一问整理的函数式求导,利用导数求出函数的单增区间和单减区间,看出变量x取到的结果.
(2)要求函数的单调性,对上一问整理的函数式求导,利用导数求出函数的单增区间和单减区间,看出变量x取到的结果.
解答:解:(1)∵∠EOA=∠FOB=2x,
∴弧EF、AE、BF的长分别为π-4x,2x,2x
连接OD,则由OD=OE=OF=1,
∠FOD=∠EOD=2x+
∴DE=DF=
=
=
(sinx+cosx),
∴y=2k(2
(sinx+cosx)+π-4x)+k(2
+4x)
=2k(2
(sinx+cosx)-2x+
+π);
(2)∵由y′=4k(
(cosx-sinx)-1)=0,
解得cos(x+
)=
,
即x=
,
又当x∈(0,
)时,y'>0,此时y在(0,
)上单调递增;
当x∈(
,
)时,y'<0,此时y在(
,
)上单调递减.
故当x=
时,该霓虹灯整体的“心悦效果”最佳.
∴弧EF、AE、BF的长分别为π-4x,2x,2x
连接OD,则由OD=OE=OF=1,
∠FOD=∠EOD=2x+
| π |
| 2 |
∴DE=DF=
1+1-2cos(2x+
|
| 2+2sin2x |
| 2 |
∴y=2k(2
| 2 |
| 2 |
=2k(2
| 2 |
| 2 |
(2)∵由y′=4k(
| 2 |
解得cos(x+
| π |
| 4 |
| 1 |
| 2 |
即x=
| π |
| 12 |
又当x∈(0,
| π |
| 12 |
| π |
| 12 |
当x∈(
| π |
| 12 |
| π |
| 4 |
| π |
| 12 |
| π |
| 4 |
故当x=
| π |
| 12 |
点评:本题是一道难度较大的题,表现在以下几个方面第一需要自己根据条件建立三角函数模型写出解析式,再对解析式进行整理运算,得到函数性质,这是一个综合题,解题的关键是读懂题意.

练习册系列答案
相关题目
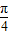 ).现在弧EF、线段DE与线段DF上装彩灯,在弧AE、弧BF、线段AD与线段BD上装节能灯.若每种灯的“心悦效果”均与相应的线段或弧的长度成正比,且彩灯的比例系数为2k,节能灯的比例系数为k(k>0),假定该霓虹灯整体的“心悦效果”y是所有灯“心悦效果”的和.
).现在弧EF、线段DE与线段DF上装彩灯,在弧AE、弧BF、线段AD与线段BD上装节能灯.若每种灯的“心悦效果”均与相应的线段或弧的长度成正比,且彩灯的比例系数为2k,节能灯的比例系数为k(k>0),假定该霓虹灯整体的“心悦效果”y是所有灯“心悦效果”的和.
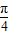 ).现在弧EF、线段DE与线段DF上装彩灯,在弧AE、弧BF、线段AD与线段BD上装节能灯.若每种灯的“心悦效果”均与相应的线段或弧的长度成正比,且彩灯的比例系数为2k,节能灯的比例系数为k(k>0),假定该霓虹灯整体的“心悦效果”y是所有灯“心悦效果”的和.
).现在弧EF、线段DE与线段DF上装彩灯,在弧AE、弧BF、线段AD与线段BD上装节能灯.若每种灯的“心悦效果”均与相应的线段或弧的长度成正比,且彩灯的比例系数为2k,节能灯的比例系数为k(k>0),假定该霓虹灯整体的“心悦效果”y是所有灯“心悦效果”的和.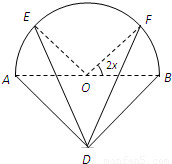
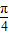 ).现在弧EF、线段DE与线段DF上装彩灯,在弧AE、弧BF、线段AD与线段BD上装节能灯.若每种灯的“心悦效果”均与相应的线段或弧的长度成正比,且彩灯的比例系数为2k,节能灯的比例系数为k(k>0),假定该霓虹灯整体的“心悦效果”y是所有灯“心悦效果”的和.
).现在弧EF、线段DE与线段DF上装彩灯,在弧AE、弧BF、线段AD与线段BD上装节能灯.若每种灯的“心悦效果”均与相应的线段或弧的长度成正比,且彩灯的比例系数为2k,节能灯的比例系数为k(k>0),假定该霓虹灯整体的“心悦效果”y是所有灯“心悦效果”的和.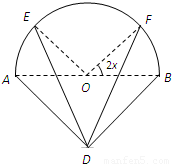
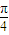 ).现在弧EF、线段DE与线段DF上装彩灯,在弧AE、弧BF、线段AD与线段BD上装节能灯.若每种灯的“心悦效果”均与相应的线段或弧的长度成正比,且彩灯的比例系数为2k,节能灯的比例系数为k(k>0),假定该霓虹灯整体的“心悦效果”y是所有灯“心悦效果”的和.
).现在弧EF、线段DE与线段DF上装彩灯,在弧AE、弧BF、线段AD与线段BD上装节能灯.若每种灯的“心悦效果”均与相应的线段或弧的长度成正比,且彩灯的比例系数为2k,节能灯的比例系数为k(k>0),假定该霓虹灯整体的“心悦效果”y是所有灯“心悦效果”的和.