题目内容

10．设函数f（x+1）=x2+2x，则f（x）的单调递减区间是（-∞，0）．

分析 先求出函数f（x）的表达式，得到函数的对称轴，从而求出函数的递减区间即可．

解答 解：∵f（x+1）=x2+2x=（x+1）2-1，
∴f（x）=x2-1，对称轴x=0，开口向上，
∴函数的递减区间是（-∞，0），
故答案为：（-∞，0）．

点评 本题考查了二次函数的性质，考查函数的单调性问题，是一道基础题．

练习册系列答案
相关题目
20．已知 A（-2，3）、B（4，-3）两点，则线段AB的中点坐标是（　　）
A．（3，0）B．（2，3）C．（3，3）D．（1，0）
1．下列函数中，为偶函数的是（　　）
A．y=x+1B．y=$\frac{1}{x}$C．y=x4D．y=x5
18．定积分 $\int_{\;1}^{\;2}{4xdx}$=（　　）
A．2B．4C．6D．8
5．已知函数y=x${\;}^{{m}^{2}-m-2}$（m∈N*）的图象与坐标轴无交点，则m的值是1，2．
15．已知数列{an}的前n项和为Sn，满足a1=tanα，（0＜α＜$\frac{π}{2}$，α≠$\frac{π}{6}$），an+1=$\frac{{a}_{n}+\sqrt{3}}{1-\sqrt{3}{a}_{n}}$（n∈N*）关于下列命题：
①若α=$\frac{π}{3}$，则a3=0；
②对任意满足条件的角α，均有an+3=an（n∈N*）
③存在α0∈（0，$\frac{π}{6}$）∪（$\frac{π}{6}$，$\frac{π}{2}$），使得S3n=0
④当$\frac{π}{6}$＜α＜$\frac{π}{3}$时，S3n＜0
其中正确的命题有（　　）
A．1 个B．2 个C．3 个D．4 个
2．已知函数f（x）=2x3-3x2-f′（0）x+c（c∈R），其中 f′（0）为函数f（x）在x=0处的导数．
（Ⅰ）求函数f（x）的递减区间；
（Ⅱ）若函数f（x）的图象关于（$\frac{1}{2}$，0）对称，求实数c的值．
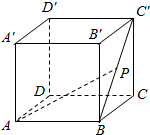19．如图，ABCD-A′B′C′D′是棱长为1的正方体，点P是BC′上的动点，$\overrightarrow{BP}=λ\overrightarrow{BC'}$，则$\overrightarrow{AP}•\overrightarrow{DC}$的值是1．
20．设函数f（x）=kax-a-x（a＞0且a≠1）是定义域为R的奇函数．
（1）若f（1）＜0，试求不等式  f（x2+2x）+f（x-4）＞0的解集；
（2）若f（1）=$\frac{3}{2}$，且g（x）=a2x+a-2x-2mf（x），x∈[1，+∞）的最小值为-2，求m的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网