题目内容
【题目】经销商经销某种农产品,在一个销售季度内,每售出1t该产品获利润500元,未售出的产品,每1t亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了130t该农产品.以X(单位:t,100≤X≤150)表示下一个销售季度内的市场需求量,T(单位:元)表示下一个销售季度内经销该农产品的利润.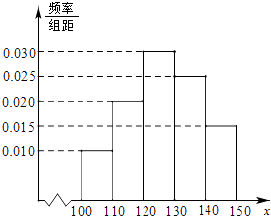
(Ⅰ)将T表示为X的函数;
(Ⅱ)根据直方图估计利润T不少于57000元的概率.
【答案】解:(I)由题意得,当X∈[100,130)时,T=500X﹣300(130﹣X)=800X﹣39000,
当X∈[130,150]时,T=500×130=65000,
∴T= ![]() .
.
(II)由(I)知,利润T不少于57000元,当且仅当120≤X≤150.
由直方图知需求量X∈[120,150]的频率为0.7,
所以下一个销售季度的利润T不少于57000元的概率的估计值为0.7.
【解析】(1)根据题意,分别写出当X∈[100,130)时,当X∈[130,150]时T与X的关系式,(2)由(I)知,利润T不少于57000元,当且仅当120≤X≤150,结合频率直方图,可得出下一个销售季度的利润T不少于57000元的概率的估计值为0.7.
【考点精析】根据题目的已知条件,利用频率分布直方图的相关知识可以得到问题的答案,需要掌握频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息.

练习册系列答案
相关题目