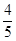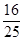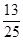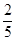题目内容
某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组:每一组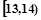 ;第二组
;第二组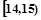 ,……,第五组
,……,第五组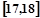 .右图是按上述分组方法得到的频率分布直方图.
.右图是按上述分组方法得到的频率分布直方图.
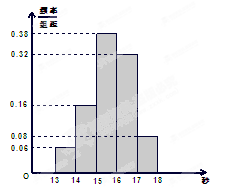
(I)若成绩大于或等于14秒且小于16秒认为良好,求该班在这次百米测试中成绩良好的人数;
(II)设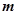 、
、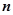 表示该班某两位同学的百米测试成绩,且已知
表示该班某两位同学的百米测试成绩,且已知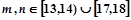 ,求事件“
,求事件“ ”的概率.
”的概率.
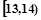 ;第二组
;第二组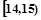 ,……,第五组
,……,第五组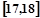 .右图是按上述分组方法得到的频率分布直方图.
.右图是按上述分组方法得到的频率分布直方图. 
(I)若成绩大于或等于14秒且小于16秒认为良好,求该班在这次百米测试中成绩良好的人数;
(II)设
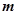 、
、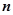 表示该班某两位同学的百米测试成绩,且已知
表示该班某两位同学的百米测试成绩,且已知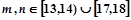 ,求事件“
,求事件“ ”的概率.
”的概率.(1)27;(2)

试题分析:(1)由直方图意义可得;(2)列举法一一列出总情况,利用古典概型公式解.
试题解析:(Ⅰ)由直方图知,成绩在
 内的人数为:
内的人数为: (人)
(人)所以该班成绩良好的人数为27人.
(Ⅱ)由直方图知,成绩在
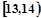 的人数为
的人数为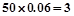 人,
人,设为
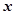 、
、 、
、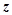 ;成绩在
;成绩在 的人数为
的人数为 人,设为
人,设为 、
、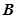 、
、 、
、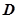 .
.若
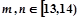 时,有
时,有 3种情况;
3种情况;若
 时,有
时,有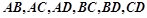 6种情况;
6种情况;若
 分别在
分别在 和
和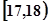 内时,
内时,| | A | B | C | D |
| x | xA | xB | xC | xD |
| y | yA | yB | yC | yD |
| z | zA | zB | zC | zD |

共有12种情况.
所以基本事件总数为21种. 记事件“
 ”为事件E,则
”为事件E,则事件E所包含的基本事件个数有12种.
∴P(E)=
 .
.即事件“
 ”的概率为
”的概率为 .
. 
练习册系列答案
相关题目

 ]上取值,则函数f(x)=ax3+bx2+ax在R上有两个相异极值点的概率是( )
]上取值,则函数f(x)=ax3+bx2+ax在R上有两个相异极值点的概率是( )
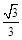
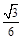
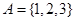 ,
,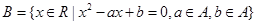 ,则
,则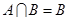 的概率是
的概率是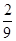
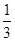
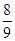
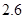
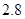
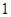 ,
,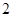 ,
,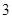 ,
,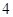 ,
,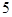 的五张卡片中任取两张,假设每张卡片被取到的概率相等,且每张卡片上只有一个数字,则取到的两张卡片上的数字之和为偶数的概率为( )
的五张卡片中任取两张,假设每张卡片被取到的概率相等,且每张卡片上只有一个数字,则取到的两张卡片上的数字之和为偶数的概率为( )