题目内容
函数f(x)=x+2cosx在区间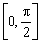 上的最大值为_________;在区间[0,2π]上最大值为___________.
上的最大值为_________;在区间[0,2π]上最大值为___________.
【答案】
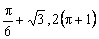

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
题目内容
函数f(x)=x+2cosx在区间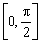 上的最大值为_________;在区间[0,2π]上最大值为___________.
上的最大值为_________;在区间[0,2π]上最大值为___________.
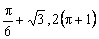

 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案