题目内容
4、求证：正四面体ABCD中相对的两棱（即异面的两棱）互相垂直．
分析：因为ABCD是正四面体，各个面都是等边三角形，取BC的中点E，则有AE⊥BC，DE⊥BC，从而有BC⊥平面AED，易得结论．
解答：证明：因为ABCD是正四面体，
各个面都是等边三角形，
取BC的中点E
∴AE⊥BC，DE⊥BC
∴BC⊥平面AED，
而AD?平面AED，
∴BC⊥AD，
同理可证AB⊥DC，AC⊥DB．
各个面都是等边三角形，
取BC的中点E
∴AE⊥BC，DE⊥BC
∴BC⊥平面AED，
而AD?平面AED，
∴BC⊥AD，
同理可证AB⊥DC，AC⊥DB．
点评：本题主要考查正四面体的结构特征，主要涉及了线线垂直，线面垂直的转化，属中档题．
练习册系列答案
星级口算天天练系列答案
相关题目
在正四面体P-ABC中，D，E，F分别是AB、BC、CA的中点，求证：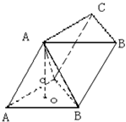
如图是各棱长均为a的斜三棱柱ABC-A1B1C1，∠A1AC=∠A1AB=60°．求证：三棱锥A1-ABC是正四面体．
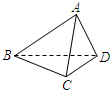如图，已知正四面体ABCD的棱长为3cm．
,
是否存在体积为V且各棱长均相等的平行六面体,使得它与棱台DEF-ABC有相同的棱长和，并且该平行六面体的一条侧棱与底面两条棱所成的角均为60°?
若存在,请具体构造出这样的一个平行六面体,并给出证明；若不存在,请说明理由.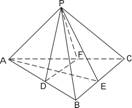
（１）BC∥平面PDF; （２）BC⊥平面PAE