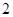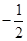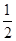题目内容
(2013·天津高考)已知首项为 的等比数列{an}的前n项和为Sn(n∈N*),且-2S2,S3,4S4成等差数列.
的等比数列{an}的前n项和为Sn(n∈N*),且-2S2,S3,4S4成等差数列.
(1)求数列{an}的通项公式.
(2)证明Sn+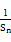 ≤
≤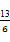 (n∈N*).
(n∈N*).
 的等比数列{an}的前n项和为Sn(n∈N*),且-2S2,S3,4S4成等差数列.
的等比数列{an}的前n项和为Sn(n∈N*),且-2S2,S3,4S4成等差数列.(1)求数列{an}的通项公式.
(2)证明Sn+
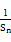 ≤
≤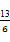 (n∈N*).
(n∈N*).(1)an= (-1)n-1·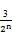 . (2)见解析
. (2)见解析
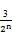 . (2)见解析
. (2)见解析(1)设等比数列{an}的公比为q,由-2S2,S3,4S4成等差数列,所以S3+2S2=4S4-S3,S4-S3=S2-S4,可得2a4=-a3,于是q=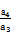 =-
=- .又a1=
.又a1= ,所以等比数列{an}的通项公式为an=
,所以等比数列{an}的通项公式为an= ×
×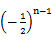 =(-1)n-1·
=(-1)n-1·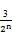 .
.
(2)Sn=1-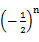 ,Sn+
,Sn+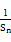 =1-
=1-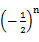 +
+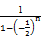 =
=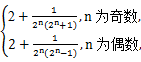
当n为奇数时,Sn+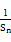 随n的增大而减小,所以Sn+
随n的增大而减小,所以Sn+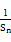 ≤S1+
≤S1+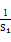 =
=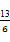 .
.
当n为偶数时,Sn+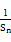 随n的增大而减小,所以Sn+
随n的增大而减小,所以Sn+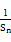 ≤S2+
≤S2+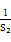 =
=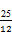 .
.
故对于n∈N*,有Sn+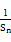 ≤
≤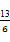 .
.
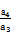 =-
=- .又a1=
.又a1= ,所以等比数列{an}的通项公式为an=
,所以等比数列{an}的通项公式为an= ×
×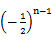 =(-1)n-1·
=(-1)n-1·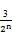 .
.(2)Sn=1-
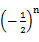 ,Sn+
,Sn+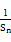 =1-
=1-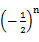 +
+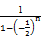 =
=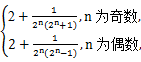
当n为奇数时,Sn+
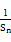 随n的增大而减小,所以Sn+
随n的增大而减小,所以Sn+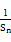 ≤S1+
≤S1+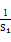 =
=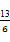 .
.当n为偶数时,Sn+
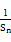 随n的增大而减小,所以Sn+
随n的增大而减小,所以Sn+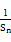 ≤S2+
≤S2+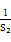 =
=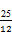 .
.故对于n∈N*,有Sn+
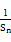 ≤
≤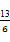 .
.
练习册系列答案
相关题目
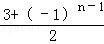 ,n∈N*,且a1=2.
,n∈N*,且a1=2.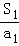 +
+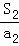 +…+
+…+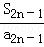 +
+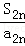 ≤n﹣
≤n﹣ (n∈N*)
(n∈N*)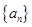 和
和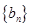 满足:
满足: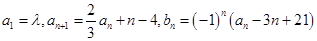 ,其中
,其中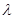 为实数,
为实数,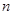 为正整数.
为正整数.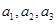 不成等比数列;
不成等比数列;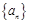 的前
的前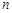 项和
项和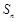 满足:
满足: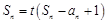 (t为常数,且
(t为常数,且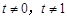 ).
).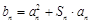 ,试求t的值,使数列
,试求t的值,使数列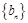 为等比数列;
为等比数列;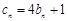 ,数列
,数列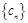 的前
的前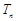 ,若不等式
,若不等式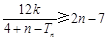 对
对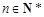 恒成立,求实数
恒成立,求实数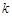 的取值范围.
的取值范围.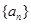 中,
中,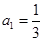 ,公比
,公比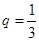 ,
,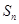 为
为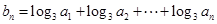 ,求数列
,求数列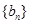 的通项公式.
的通项公式. ________.
________.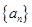 中,
中,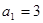 且
且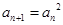 (
(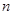 是正整数),则数列的通项公式
是正整数),则数列的通项公式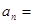 .
.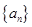 中,
中,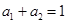 ,
,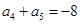 ,则公比
,则公比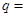 ( )
( )