题目内容
在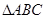 中,角
中,角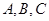 的对边分别为
的对边分别为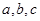 ,且
,且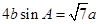 .
.
(1)求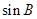 的值;
的值;
(2)若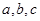 成等差数列,且公差大于0,求
成等差数列,且公差大于0,求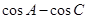 的值.
的值.
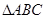 中,角
中,角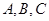 的对边分别为
的对边分别为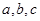 ,且
,且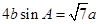 .
.(1)求
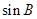 的值;
的值;(2)若
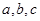 成等差数列,且公差大于0,求
成等差数列,且公差大于0,求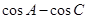 的值.
的值.(1) ;(2)
;(2) .
.
 ;(2)
;(2) .
.试题分析:本题主要考查解三角形中的正弦定理与数列的综合问题、利用正弦定理求三角函数值、等差数列的性质、三角函数值问题等基础知识,同时考查运算转化能力和计算能力.第一问,根据正弦定理将边转换成角,即可得到
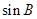 ;第二问,利用等差中项的概念得
;第二问,利用等差中项的概念得 ,再利用正弦定理将边转换成角,得到
,再利用正弦定理将边转换成角,得到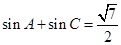 ,设
,设 ,两式联立,利用平方关系和两角和的余弦公式,得到
,两式联立,利用平方关系和两角和的余弦公式,得到 ,再利用内角和与诱导公式,将
,再利用内角和与诱导公式,将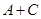 转化成
转化成 ,解方程求出
,解方程求出 的值,即
的值,即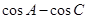 的值.
的值.试题解析:(Ⅰ)由
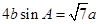 ,根据正弦定理得
,根据正弦定理得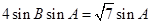 ,
,所以
 . 4分
. 4分(Ⅱ)由已知和正弦定理以及(Ⅰ)得
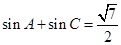 . ①
. ①设
 , ②
, ②①2+②2,得
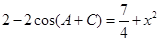 . ③ 7分
. ③ 7分又
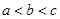 ,
, ,所以
,所以 ,
, ,
,故
 . 10分
. 10分代入③式得
 .
.因此
 .
.
练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
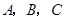 的三内角
的三内角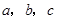 ,且
,且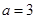 ,A=
,A=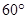 ,
,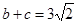 .
.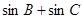 的值及
的值及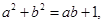 以AB为边向△ABC外作等边三角形△ABD.
以AB为边向△ABC外作等边三角形△ABD.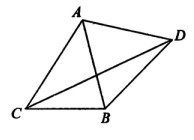
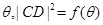 .试求函数
.试求函数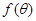 的最大值及
的最大值及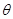 的值.
的值.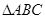 中,角
中,角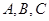 所对的边分别为
所对的边分别为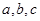 ,函数
,函数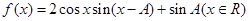 在
在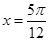 处取得最大值.
处取得最大值.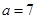 且
且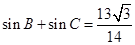 ,求
,求 中,角
中,角 的对边分别为
的对边分别为 ,已知
,已知 ,
,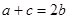 ;
; ,求
,求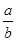 的值.
的值.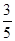 .
.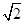 ,b=5,求向量
,b=5,求向量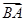 在
在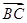 方向上的投影.
方向上的投影.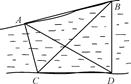
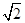 (B)2
(B)2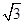 (C)
(C)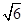 -
-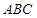 中,三个内角
中,三个内角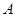 ,
,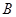 ,
,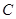 所对的边分别为
所对的边分别为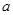 ,
,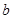 ,
,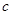 ,若
,若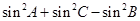
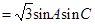 ,则
,则