题目内容
已知非零实数a,b满足a,
,b成等比数列,则ab的取值范围是( )
| 4 | a2+b2 |
分析:由a,
,b成等比数列,利用等比数列的性质列出关系式,整理化简后利用基本不等式得出关于ab的不等式,求出不等式的解集可得出ab的范围.
| 4 | a2+b2 |
解答:解:∵a,
,b成等比数列,
∴(
)2=
=ab>0,
又a2+b2≥2ab,当且仅当a=b时取等号,
∴ab≥
,即(ab)2-2ab≥0,
分解因式得:ab(ab-2)≥0,
解得:ab≤0(舍去)或ab≥2,
则ab的取值范围是[2,+∞).
故选C
| 4 | a2+b2 |
∴(
| 4 | a2+b2 |
| a2+b2 |
又a2+b2≥2ab,当且仅当a=b时取等号,
∴ab≥
| 2ab |
分解因式得:ab(ab-2)≥0,
解得:ab≤0(舍去)或ab≥2,
则ab的取值范围是[2,+∞).
故选C
点评:此题考查了等比数列的性质,基本不等式的运用,以及一元二次不等式的解法,熟练掌握等比数列的性质是解本题的关键.

练习册系列答案
相关题目
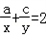 ,求证:非零实数a,b,c成等比数列.
,求证:非零实数a,b,c成等比数列.