题目内容
设f(x)=px-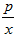 -2lnx.
-2lnx.
(1)若f(x)在其定义域内为单调递增函数,求实数p的取值范围;
(2)设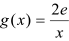 ,且p>0,若在[1,e]上至少存在一点x0,使得f(x0)>g(x0)成立,求实数p的取值范围。
,且p>0,若在[1,e]上至少存在一点x0,使得f(x0)>g(x0)成立,求实数p的取值范围。
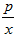 -2lnx.
-2lnx. (1)若f(x)在其定义域内为单调递增函数,求实数p的取值范围;
(2)设
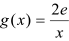 ,且p>0,若在[1,e]上至少存在一点x0,使得f(x0)>g(x0)成立,求实数p的取值范围。
,且p>0,若在[1,e]上至少存在一点x0,使得f(x0)>g(x0)成立,求实数p的取值范围。解:
(1)由已知得: ,
,
要使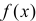 在其定义域(0,+∞)为单调递增函数,只需
在其定义域(0,+∞)为单调递增函数,只需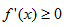 ,即px2-2x+p≥0在(0,+∞)上恒成立, 显然p>0,且h(x)=px2-2x+p的对称轴为
,即px2-2x+p≥0在(0,+∞)上恒成立, 显然p>0,且h(x)=px2-2x+p的对称轴为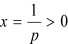 ,
,
故△=4-4p2≤0,解得p≥1。
(2)原命题等价于f(x)-g(x)>0在[1,e]上有解,
设F(x)=f(x)-g(x)
∵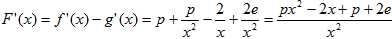
=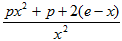 >0
>0
F(x)在[1,e]上是增函数,
∴F(x)max= F(e)>0 ,
解得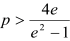 ,
,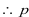 的取值范围是
的取值范围是 .
.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目