题目内容
设f(x)=px(1)求p与q的关系;
(2)若f(x)在其定义域内为单调递增函数,求p的取值范围;
(3)设g(x)=![]() 且p>0,若在[1,e]上至少存在一点x0,使得f(x0)>g(x0)成立,求实数p的取值范围.
且p>0,若在[1,e]上至少存在一点x0,使得f(x0)>g(x0)成立,求实数p的取值范围.
解:(1)由题意得f(e)=pe![]() -2lne=qe
-2lne=qe![]() -2
-2![]() (p-q)(e+
(p-q)(e+![]() )=0.而e+
)=0.而e+![]() ≠0,∴p=q.
≠0,∴p=q.
(2)由(1)知f(x)=px![]() -2lnx,f′(x)=p+
-2lnx,f′(x)=p+![]() ,要使f(x)在其定义域(0,+∞)内为单调增函数,只需f′(x)在(0,+∞)内满足f′(x)≥0恒成立,即px2-2x+p≥0(p>0)对x∈(0,+∞)恒成立,即p≥
,要使f(x)在其定义域(0,+∞)内为单调增函数,只需f′(x)在(0,+∞)内满足f′(x)≥0恒成立,即px2-2x+p≥0(p>0)对x∈(0,+∞)恒成立,即p≥![]() .令h(x)=
.令h(x)=![]() (x>0),则h(x)=
(x>0),则h(x)=![]() ≤1.
≤1.
∴p≥1.
(3)∵g(x)=![]() 在[1,e]上是减函数,
在[1,e]上是减函数,
∴x=e时,g(x)min=2,x=1时,g(x)max=2e,即g(x)∈[2,2e].
①当0<p<1时,由x∈[1,e]![]() x
x![]() ≥0,
≥0,
∴f(x)=p(x![]() )-2lnx<x
)-2lnx<x![]() -2lnx.又由(1)得y=x
-2lnx.又由(1)得y=x![]() -2lnx在[1,e]上单调递增,∴f(x)<x
-2lnx在[1,e]上单调递增,∴f(x)<x![]() -2lnx≤e
-2lnx≤e![]() -2lne=e
-2lne=e![]() -2<2,不合题意.
-2<2,不合题意.
②当p≥1时,由(2)知f(x)在[1,e]上单调递增,又g(x)在[1,e]上是减函数.∴本命题f(x)max>g(x)min=2,x∈[1,e].
又f(x)max=f(e)=p(e![]() )-2lne,∴p(e
)-2lne,∴p(e![]() )-2lne>2
)-2lne>2![]() p>
p>![]() .
.
综上,p的取值范围是(![]() ,+∞).
,+∞).

练习册系列答案
相关题目
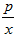 -2lnx.
-2lnx. 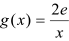 ,且p>0,若在[1,e]上至少存在一点x0,使得f(x0)>g(x0)成立,求实数p的取值范围。
,且p>0,若在[1,e]上至少存在一点x0,使得f(x0)>g(x0)成立,求实数p的取值范围。