题目内容
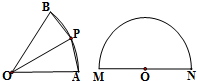 已知扇形OAB,点P为弧AB上异于A,B的任意一点,当P为弧AB的中点时,S△OAP+S△OBP的值最大.现有半径为R的半圆O,在圆弧MN上依次取点P1,P2,…,P2n-1(异于M,N),则S△OMP1+S△OP1P2+…+S△OP2n-1N的最大值为
已知扇形OAB,点P为弧AB上异于A,B的任意一点,当P为弧AB的中点时,S△OAP+S△OBP的值最大.现有半径为R的半圆O,在圆弧MN上依次取点P1,P2,…,P2n-1(异于M,N),则S△OMP1+S△OP1P2+…+S△OP2n-1N的最大值为2n-1R2sin
| π |
| 2n |
2n-1R2sin
.| π |
| 2n |
分析:利用三角形的面积计算公式和数学归纳法即可得出.
解答:解:S△OMP1+S△OP1P2+…+S△OP2n-1N=
R2(sin∠MOP1+sin∠P1OP2+…+sin∠P2n-1ON),
设∠MOP1=θ1,∠P1OP2=θ2,…,∠P2n-1ON=θ2n.则θ1+θ2+…+θ2n=π.
∵0<θi<π,∴sinθi>0,
猜想S△OMP1+S△OP1P2+…+S△OP2n-1N的最大值为2n-1R2sin
.
即
R2(sinθ1+sinθ2+…+sinθn)≤2nR2sin
?sinθ1+sinθ2+…+sinθ2n≤2nsin
(θ1+θ2+…+θ2n=π).
下面用数学归纳法证明:
(1)当n=1时,由扇形OAB,点P为弧AB上异于A,B的任意一点,当P为弧AB的中点时,S△OAP+S△OBP的值最大,可知成立.
(2)假设当n=k(k∈N*)时,不等式成立,即sinθ1+sinθ2+…+sinθ2k≤2ksin
.成立.(θ1+θ2+…+θ2k=π,θi>0)
则当n=k+1时,左边=即sinθ1+sinθ2+…+sinθ2k+sinθ2k+1+…+sinθ2k+1
∵sinθi+sinθi+1=2sin
cos
≤2sin
,当且仅当θi=θi+1时取等号.
∴左边≤2sin
+2sin
+…+2sin
≤2•2ksin
=2k+1sin
=右边,当且仅当θi=θi+1(i∈N*,且1≤i≤2k+1-1)时取等号.
即不等式对于?n∈N*都成立.
故答案为2n-1R2sin
.
| 1 |
| 2 |
设∠MOP1=θ1,∠P1OP2=θ2,…,∠P2n-1ON=θ2n.则θ1+θ2+…+θ2n=π.
∵0<θi<π,∴sinθi>0,
猜想S△OMP1+S△OP1P2+…+S△OP2n-1N的最大值为2n-1R2sin
| π |
| 2n |
即
| 1 |
| 2 |
| π |
| 2n |
| π |
| 2n |
下面用数学归纳法证明:
(1)当n=1时,由扇形OAB,点P为弧AB上异于A,B的任意一点,当P为弧AB的中点时,S△OAP+S△OBP的值最大,可知成立.
(2)假设当n=k(k∈N*)时,不等式成立,即sinθ1+sinθ2+…+sinθ2k≤2ksin
| π |
| 2k |
则当n=k+1时,左边=即sinθ1+sinθ2+…+sinθ2k+sinθ2k+1+…+sinθ2k+1
∵sinθi+sinθi+1=2sin
| θi+θi+1 |
| 2 |
| θi-θi+1 |
| 2 |
| θi+θi+1 |
| 2 |
∴左边≤2sin
| θ1+θ2 |
| 2 |
| θ3+θ4 |
| 2 |
| θ2k+1-1+θ2k+1 |
| 2 |
≤2•2ksin
| π |
| 2k+1 |
| π |
| 2k+1 |
即不等式对于?n∈N*都成立.
故答案为2n-1R2sin
| π |
| 2n |
点评:熟练掌握三角形的面积计算公式和数学归纳法是解题的关键.

练习册系列答案
相关题目
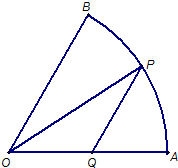 已知扇形OAB的半径为3,圆心角∠AOB=60°,过弧AB上的动点P作平行于BO的直线交AO于点Q,设∠AOP=θ.
已知扇形OAB的半径为3,圆心角∠AOB=60°,过弧AB上的动点P作平行于BO的直线交AO于点Q,设∠AOP=θ.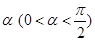 ,半径为R,P为弧AB上的动点,过P作PQ//OB交OA于Q,则
,半径为R,P为弧AB上的动点,过P作PQ//OB交OA于Q,则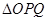 面积最大值等于
面积最大值等于
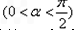 ,半径为R,P为弧AB上的动点,过P作PQ∥OB交OA于Q,则△OPQ面积最大值等于( )
,半径为R,P为弧AB上的动点,过P作PQ∥OB交OA于Q,则△OPQ面积最大值等于( )