题目内容
(本题满分12分)
已知整数列 满足
满足 ,
, ,前
,前 项依次成等差数列,从第
项依次成等差数列,从第 项起依次成等比数列.
项起依次成等比数列.
(1)求数列 的通项公式;
的通项公式;
(2)求出所有的正整数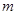 ,使得
,使得 .
.
已知整数列
 满足
满足 ,
, ,前
,前 项依次成等差数列,从第
项依次成等差数列,从第 项起依次成等比数列.
项起依次成等比数列.(1)求数列
 的通项公式;
的通项公式;(2)求出所有的正整数
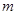 ,使得
,使得 .
.解:(1) 设数列前6项的公差为d,则a5=-1+2d,a6=-1+3d,d为整数.
又a5,a6,a7成等比数列,所以(3d-1)2=4(2d-1),
即 9d2-14d+5=0,得d ="1. " …………………3分
当n≤6时,an =n-4,
由此a5=1,a6=2,数列从第5项起构成的等比数列的公比为2,
所以,当n≥5时,an =2n-5.
故
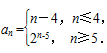 …………………6分
…………………6分(2) 由(1)知,数列
 为:-3,-2,-1,0,1,2,4,8,16,…
为:-3,-2,-1,0,1,2,4,8,16,…当m=1时等式成立,即-3-2-1=―6=(-3)(-2)(-1);
当m=3时等式成立,即-1+0+1=0;
当m=2、4时等式不成立; …………………9分
当m≥5时,amam+1am+2=23m-12,am +am+1+am+2=2m-5(23-1)=7×2m-5,
7×2m-5≠23m-12,
所以am +am+1+am+2≠amam+1am+2 .
故所求m= 1,或m=3. …………………12分
略

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 列
列 中,
中, ,且
,且 是
是 和
和 的等差中项.
的等差中项. )求数列
)求数列 满足
满足 ,求
,求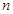 项和
项和 .
. 的首项为
的首项为 ,公差为
,公差为 ,前n项的和为Sn,则数列
,前n项的和为Sn,则数列 为等差数列,且通项为
为等差数列,且通项为 .类似地,请完成下列命题:若各项均为正数的等比数列
.类似地,请完成下列命题:若各项均为正数的等比数列 的首项为
的首项为 ,公比为
,公比为 ,前
,前 项的积为Tn,则
项的积为Tn,则  的前n项和为Sn,且
的前n项和为Sn,且 则过点
则过点 的直线的斜率是______________
的直线的斜率是______________ 中前
中前 项和为
项和为 ,已知
,已知 ,
, ,则
,则
 满足:
满足: ,且
,且
 满足:
满足: ,求数列
,求数列 中,
中, 则
则 =
=  中,
中, 则
则 ( )
( )


