题目内容
已知随机变量ξ+η=8,若ξ~B(10,0.6),则Eη,Dη分别是( )
| A.6和2.4 | B.2和2.4 | C.2和5.6 | D.6和5.6 |
B
解:因为Eξ=10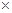 0.6=6,Dξ=10
0.6=6,Dξ=10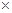 0.6
0.6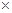 0.4=2.4Eη=E(8-ξ)=8-6=2,Dη= Dξ=2.4
0.4=2.4Eη=E(8-ξ)=8-6=2,Dη= Dξ=2.4
 0.6=6,Dξ=10
0.6=6,Dξ=10 0.6
0.6 0.4=2.4Eη=E(8-ξ)=8-6=2,Dη= Dξ=2.4
0.4=2.4Eη=E(8-ξ)=8-6=2,Dη= Dξ=2.4
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
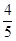 ,第二、第三种产品受欢迎的概率分别为
,第二、第三种产品受欢迎的概率分别为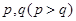 ,且不同种产品是否受欢迎相互独立.记
,且不同种产品是否受欢迎相互独立.记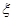 为公司向市场投放三种新型产品受欢迎的数量,其分布列为
为公司向市场投放三种新型产品受欢迎的数量,其分布列为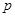
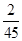
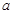
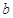
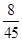
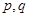 的值
的值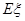 .
.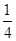 ,不堵车的概率为
,不堵车的概率为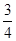 ;汽车走公路②堵车的概率为
;汽车走公路②堵车的概率为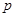 ,不堵车的概率为
,不堵车的概率为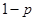 ,若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响。(I)若三辆车中恰有一辆车被堵的概率为
,若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响。(I)若三辆车中恰有一辆车被堵的概率为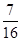 ,求走公路②堵车的概率;(Ⅱ)在(I)的条件下,求三辆车中被堵车辆的个数
,求走公路②堵车的概率;(Ⅱ)在(I)的条件下,求三辆车中被堵车辆的个数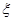 的分布列和数学期望。
的分布列和数学期望。 元奖金.假设顾客每次抽奖时获奖与否的概率都是
元奖金.假设顾客每次抽奖时获奖与否的概率都是 ,
, 元的概率;
元的概率; .请写出
.请写出 为小球编号与盒子编号不一致的数目,则
为小球编号与盒子编号不一致的数目,则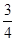
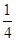
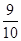
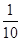
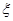 的分布列为下表所示:
的分布列为下表所示: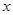
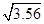 C.3.2 D.
C.3.2 D.