题目内容
【题目】如果数列![]() ,
,![]() ,
,![]() ,
,![]() (
(![]() ,且
,且![]() ),满足:①
),满足:①![]() ,
,![]() ;
;
②![]() ,那么称数列
,那么称数列![]() 为“
为“![]() ”数列.
”数列.
(![]() )已知数列
)已知数列![]() ,
,![]() ,
,![]() ,
,![]() ;数列
;数列![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .试判断数列
.试判断数列![]() ,
,![]() 是否为“
是否为“![]() ”数列.
”数列.
(![]() )是否存在一个等差数列是“
)是否存在一个等差数列是“![]() ”数列?请证明你的结论.
”数列?请证明你的结论.
(![]() )如果数列
)如果数列![]() 是“
是“![]() ”数列,求证:数列
”数列,求证:数列![]() 中必定存在若干项之和为
中必定存在若干项之和为![]() .
.
【答案】(![]() )数列
)数列![]() 不是“
不是“![]() ”数列,数列
”数列,数列![]() 是“
是“![]() ”数列;(
”数列;(![]() )不存在等差数列是“
)不存在等差数列是“![]() ”数列;(
”数列;(![]() )证明见解析.
)证明见解析.
【解析】分析:(1)根据定义直接判断即可得解;(2)假设存在等差数列是“![]() ”数列,由
”数列,由![]() ,得
,得![]() ,与
,与![]() 矛盾,从而可证不存在等差数列为“
矛盾,从而可证不存在等差数列为“![]() ”数列;(3)将数列
”数列;(3)将数列![]() 按以下方法重新排列:设
按以下方法重新排列:设![]() 为重新排列后所得数列的前
为重新排列后所得数列的前![]() 项和(
项和(![]() 且
且![]() ),任取大于0的一项作为第一项,则满足
),任取大于0的一项作为第一项,则满足![]() ,然后利用反证法,证明即可.
,然后利用反证法,证明即可.
详解:(![]() )由题目是
)由题目是![]() 定义可直接判断出,数列
定义可直接判断出,数列![]() 不符合
不符合![]() 数列要求,数列
数列要求,数列![]() 是“
是“![]() ”数列.
”数列.
(![]() )不存在一个等差数列是“
)不存在一个等差数列是“![]() ”数列,
”数列,
证明:假设存在等差数列是“![]() ”数列,
”数列,
则由![]() ,得
,得![]() 与
与![]() 矛盾,
矛盾,
说明假设不成立,即不存在等差数列是“![]() ”数列.
”数列.
(![]() )将数列
)将数列![]() 按以下方法重新排列:
按以下方法重新排列:
设![]() 为重新排列后所得数列的前
为重新排列后所得数列的前![]() 项和(
项和(![]() ,且
,且![]() ),
),
任取大于![]() 的一项作为第一项,则满足
的一项作为第一项,则满足![]() ,
,
假设当![]() 时,
时,![]() ,
,
若![]() ,则任取大于
,则任取大于![]() 的一项作为第
的一项作为第![]() 项,可保证
项,可保证![]() ,
,
若![]() ,则剩下的项必有
,则剩下的项必有![]() 或与
或与![]() 异号的一项,否则总和不是
异号的一项,否则总和不是![]() ,
,
∴取![]() 或与
或与![]() 异号的一项作为第
异号的一项作为第![]() 项,可保证
项,可保证![]() ,
,
如果按上述排列后存在![]() 成立,那么命题得证,
成立,那么命题得证,
否则![]() ,
,![]() ,
,![]()
![]() 这
这![]() 个整数只能取区间
个整数只能取区间![]() 内的非
内的非![]() 整数,
整数,
∵区间![]() 内的非
内的非![]() 整数至多
整数至多![]() 个,
个,
∴一定存在![]() ,
,
那么从第![]() 项到第
项到第![]() 项之和为
项之和为![]() ,命题得证,
,命题得证,
综上所述,数列![]() 中一定存在若干项之和为
中一定存在若干项之和为![]() ,证毕.
,证毕.

 阅读快车系列答案
阅读快车系列答案【题目】某商场举行有奖促销活动,顾客购买一定金额的商品后即可参加一次抽奖.随着抽奖活动的有效开展,参与抽奖活动的人数越来越多,该商场对前5天抽奖活动的人数进行统计,y表示第x天参加抽奖活动的人数,得到统计表如下:
x | 1 | 2 | 3 | 4 | 5 |
y | 50 | 60 | 70 | 80 | 100 |
经过进一步统计分析,发现y与x具有线性相关关系.
(1)若从这5天随机抽取两天,求至少有1天参加抽奖人数超过70的概率;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() ,并估计该活动持续7天,共有多少名顾客参加抽奖?
,并估计该活动持续7天,共有多少名顾客参加抽奖?
参考公式及数据: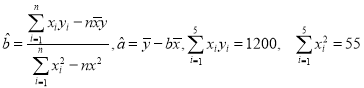 .
.