题目内容
已知不等式ax2+bx+c＜0的解集为{x|-2＜x＜1}，则不等式cx2+bx+a＞c（2x-1）+b的解集为
- A.{x|-2＜x＜1}
- B.{x|-1＜x＜2}
- C.
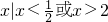
- D.
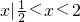
D
分析：由不等式ax2+bx+c＜0的解集为{x|-2＜x＜1}，求出a，b，c的关系，a的符号，然后化简不等式cx2+bx+a＞c（2x-1）+b求解即可．
解答：不等式ax2+bx+c＜0的解集为{x|-2＜x＜1}，a＞0
所以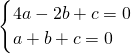
，所以3a-3b=0
a=b，c=-2a；
代入cx2+bx+a＞c（2x-1）+b
得-2ax2+ax+a＞-2a（2x-1）+a
解得x∈（
，2）
故选D．
点评：本题考查一元二次不等式的应用，考查计算能力，是基础题．
分析：由不等式ax2+bx+c＜0的解集为{x|-2＜x＜1}，求出a，b，c的关系，a的符号，然后化简不等式cx2+bx+a＞c（2x-1）+b求解即可．
解答：不等式ax2+bx+c＜0的解集为{x|-2＜x＜1}，a＞0
所以
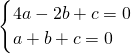，所以3a-3b=0a=b，c=-2a；
代入cx2+bx+a＞c（2x-1）+b
得-2ax2+ax+a＞-2a（2x-1）+a
解得x∈（
，2）故选D．
点评：本题考查一元二次不等式的应用，考查计算能力，是基础题．
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目