题目内容
已知an=n·0.9n(n∈N*),
(1)判断{an}的单调性;
(2)是否存在最小正整数k,使an<k对于n∈N* 恒成立?
(1)判断{an}的单调性;
(2)是否存在最小正整数k,使an<k对于n∈N* 恒成立?
解:(1)an+1-an=(n+1)·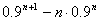 =(0.9-0.1n)·0.9n,
=(0.9-0.1n)·0.9n,
∴当n<9时,an+1>an;当n=9时,an+1=an;当n>9时,an+1<an,
∴a1,a2,…,a9单调递增,a9=a10,
a10,a11,…单调递减;
(2)由(1)知,an中a9和a10相等且最大,则数列中的最大项为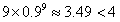 ,
,
∴存在最小正整数k=4,使an<4对n∈N*恒成立。
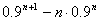 =(0.9-0.1n)·0.9n,
=(0.9-0.1n)·0.9n, ∴当n<9时,an+1>an;当n=9时,an+1=an;当n>9时,an+1<an,
∴a1,a2,…,a9单调递增,a9=a10,
a10,a11,…单调递减;
(2)由(1)知,an中a9和a10相等且最大,则数列中的最大项为
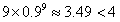 ,
,∴存在最小正整数k=4,使an<4对n∈N*恒成立。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
等差数列{an}的前n项和为Sn,已知an-1+an+1-an2=0,S2n-1=38,则n=( )
| A、38 | B、20 | C、10 | D、9 |