题目内容
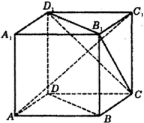 如图,ABCD-A1B1C1D1为正方体,下面结论错误的是( )
如图,ABCD-A1B1C1D1为正方体,下面结论错误的是( )分析:对于A,找出异面直线AD与CB1所成角判断正误;对于B找出异面直线AC1与BD所成角,即可判断正误;对于C通过直线与平面的垂直,判断即可;对于D通过直线与平面平行判断即可.
解答: 解:对于A,异面直线AD与CB1所成角就是∠A1DA=45°,正确;
解:对于A,异面直线AD与CB1所成角就是∠A1DA=45°,正确;
对于B,因为直线bd与平面ACC1垂直,所以异面直线AC1与BD所成角为90°,所以不正确;
对于C,由正方体的性质得 AC⊥BD,而AC是AC1在底面ABCD内的射影,由三垂线定理知,AC1⊥BD,所以AC1⊥平面CB1D1,正确;
对于D,因为BD∥B1D1,所以BD∥平面CB1D1正确;
故选B.
 解:对于A,异面直线AD与CB1所成角就是∠A1DA=45°,正确;
解:对于A,异面直线AD与CB1所成角就是∠A1DA=45°,正确;对于B,因为直线bd与平面ACC1垂直,所以异面直线AC1与BD所成角为90°,所以不正确;
对于C,由正方体的性质得 AC⊥BD,而AC是AC1在底面ABCD内的射影,由三垂线定理知,AC1⊥BD,所以AC1⊥平面CB1D1,正确;
对于D,因为BD∥B1D1,所以BD∥平面CB1D1正确;
故选B.
点评:本题考查线面平行的判定,利用三垂线定理证明直线与平面垂直,求异面直线成的角.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
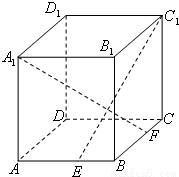
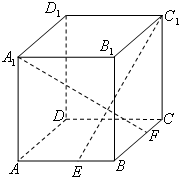 如图,ABCD-A1B1C1D1是棱长为6的正方体,E、F分别是棱AB、BC上的动点,且AE=BF.
如图,ABCD-A1B1C1D1是棱长为6的正方体,E、F分别是棱AB、BC上的动点,且AE=BF. 如图,ABCD-A1B1C1D1为正方体,下面结论中正确的是
如图,ABCD-A1B1C1D1为正方体,下面结论中正确的是 如图,ABCD-A1B1C1D1为正方体,下面结论中正确的结论是
如图,ABCD-A1B1C1D1为正方体,下面结论中正确的结论是