题目内容
已知△ABC满足c2-a2+ba-b2=0，则角C的大小为（ ）
分析：由已知等式，化简得ab=a2+b2-c2，再用余弦定理解出cosC=
，结合C∈（0，π）即可算出C的大小．
| 1 |
| 2 |
解答：解：∵c2-a2+ba-b2=0，可得ab=a2+b2-c2，
∴由余弦定理，得cosC=
=
∵C∈（0，π），∴C=
故选：A
∴由余弦定理，得cosC=
| a2+b2-c2 |
| 2ab |
| 1 |
| 2 |
∵C∈（0，π），∴C=
| π |
| 3 |
故选：A
点评：本题给出三角形边之间的平方关系，求角C的大小．着重考查了利用余弦定理解三角形的知识，属于基础题．
练习册系列答案
相关题目
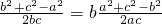?a2（b2+c2-a2）=b2（a2+c2-b2）?（a2-b2）•c2=（a2-b2）（a2+b2）?c2=a2+b2
?a2（b2+c2-a2）=b2（a2+c2-b2）?（a2-b2）•c2=（a2-b2）（a2+b2）?c2=a2+b2
?a2（b2+c2-a2）=b2（a2+c2-b2）?（a2-b2）•c2=（a2-b2）（a2+b2）?c2=a2+b2