题目内容
给出问题:已知△ABC满足a•cosA=b•cosB,试判断△ABC的形状,某学生的解答如下:
(i)a•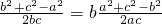 ?a2(b2+c2-a2)=b2(a2+c2-b2)?(a2-b2)•c2=(a2-b2)(a2+b2)?c2=a2+b2
?a2(b2+c2-a2)=b2(a2+c2-b2)?(a2-b2)•c2=(a2-b2)(a2+b2)?c2=a2+b2
故△ABC是直角三角形.
(ii)设△ABC外接圆半径为R,由正弦定理可得,原式等价于2RsinAcosA=2RsinBcosB?sin2A=cos2B?A=B
故△ABC是等腰三角形.
综上可知,△ABC是等腰直角三角形.
请问:该学生的解答是否正确?若正确,请在下面横线中写出解题过程中主要用到的思想方法;若不正确,请在下面横线中写出你认为本题正确的结果________.
等腰或直角三角形
分析:(i)利用余弦定理将角化为边,即可得到结论;(ii)由正弦定理,将边化为角,可得结论.
解答:不正确,解答的两种方法都可得出结论,但都不完整.
(i)a•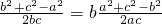 ?a2(b2+c2-a2)=b2(a2+c2-b2)?(a2-b2)•c2=(a2-b2)(a2+b2)?c2=a2+b2或a2-b2=0,故△ABC是等腰或直角三角形;
?a2(b2+c2-a2)=b2(a2+c2-b2)?(a2-b2)•c2=(a2-b2)(a2+b2)?c2=a2+b2或a2-b2=0,故△ABC是等腰或直角三角形;
(ii)设△ABC外接圆半径为R,由正弦定理可得,原式等价于2RsinAcosA=2RsinBcosB?sin2A=sin2B?A=B或A+B= ,故△ABC是等腰或直角三角形;
,故△ABC是等腰或直角三角形;
故答案为:等腰或直角三角形
点评:本题考查三角形形状的判断,解题的关键是利用余弦定理、正弦定理进行边角互化.
分析:(i)利用余弦定理将角化为边,即可得到结论;(ii)由正弦定理,将边化为角,可得结论.
解答:不正确,解答的两种方法都可得出结论,但都不完整.
(i)a•
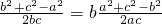 ?a2(b2+c2-a2)=b2(a2+c2-b2)?(a2-b2)•c2=(a2-b2)(a2+b2)?c2=a2+b2或a2-b2=0,故△ABC是等腰或直角三角形;
?a2(b2+c2-a2)=b2(a2+c2-b2)?(a2-b2)•c2=(a2-b2)(a2+b2)?c2=a2+b2或a2-b2=0,故△ABC是等腰或直角三角形;(ii)设△ABC外接圆半径为R,由正弦定理可得,原式等价于2RsinAcosA=2RsinBcosB?sin2A=sin2B?A=B或A+B=
 ,故△ABC是等腰或直角三角形;
,故△ABC是等腰或直角三角形;故答案为:等腰或直角三角形
点评:本题考查三角形形状的判断,解题的关键是利用余弦定理、正弦定理进行边角互化.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目


 ?a2(b2+c2-a2)=b2(a2+c2-b2)?(a2-b2)•c2=(a2-b2)(a2+b2)?c2=a2+b2
?a2(b2+c2-a2)=b2(a2+c2-b2)?(a2-b2)•c2=(a2-b2)(a2+b2)?c2=a2+b2 ?a2(b2+c2-a2)=b2(a2+c2-b2)?(a2-b2)•c2=(a2-b2)(a2+b2)?c2=a2+b2
?a2(b2+c2-a2)=b2(a2+c2-b2)?(a2-b2)•c2=(a2-b2)(a2+b2)?c2=a2+b2