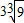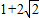Question

已知x+3y-2=0，则3^x+27^y+1的最小值为

 

．（x=

 

；y=

 

）

Answer 1

分析：将x用y表示出来，代入3^x+27^y+1，化简整理后用基本不等式求最小值．

解答：解：由x+3y-2=0得x=2-3y
代入3^x+27^y+1=3^2-3y+27^y+1=

9

27y

+27^y+1≥7
当

9

27y

=27^y时，即y=

1

3

，x=1时等号成立
故3^x+27^y+1的最小值为7
故答案为：7；1；

1

3

．

点评：考查基本不等式求最值，本题通过观察将其转化为积为最值的形式，才可求最小值．