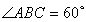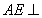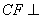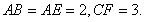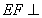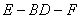题目内容
如图,菱形ABCD中,∠DAB=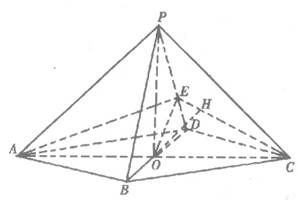
(Ⅰ)证明:PD⊥平面EAC;
(Ⅱ)求二面角A-PD-C的余弦值;
(Ⅲ)求点B到平面PDC的距离.
解法一:(Ⅰ)∵PO⊥平面ABCD,∴OD为PD在平面ABCD内的阴影

又ABCD为菱形,∴AC⊥OD,∴AC⊥PD,即PD⊥AC
在菱形ABCD中,∵∠DAB=60°
∴OD=AO·cot60°=1
在Rt△POD中,PD=![]() =2,由PE:ED=3:1,
=2,由PE:ED=3:1,
得OE=![]() P D=
P D=![]() ,又∠PDO=6 0°,
,又∠PDO=6 0°,
∴OE2=OD2+DE2-2OD·DEcos60°=![]()
∴OE2+DE2=OD2, ∴∠OED=90°,即PD⊥OE
(Ⅱ)由(Ⅰ)知PD⊥EA,PD⊥EC,则∠AEC为二面角A-PD-C的平面角
tan∠AEO=![]() =2,易知OE为AC的垂直平分线,所以∠AEC=2∠AEO,
=2,易知OE为AC的垂直平分线,所以∠AEC=2∠AEO,
∴cos∠AEC=cos2∠AEO-sin2∠AEO
=![]()
=![]()
(Ⅲ)由O为BD中点,知点B到平面PDC的距离等于点O到平面PDC距离的2倍,由(Ⅰ)知,平面OEC⊥平面PDC,作OH⊥CE,垂足为H,则OH⊥平面PDC,在Rt△OEC中,∠EOC=90°,OC=![]() ,OE=
,OE=![]() ,
,
∴OH=![]()
所以点B到平面PDC的距离为![]() .
.
解法二:建立如图所示的坐标系O-xyz,其中A(0,-![]() ,0),B(1,0,0),C(0,
,0),B(1,0,0),C(0,![]() ,0),D(-1,0,0),
,0),D(-1,0,0),
P(0,0,![]() ).
).

(Ⅰ)由PE:ED=3:1,知E(-![]() )
)
∵![]() =(1,0,
=(1,0,![]() ),
),![]() =(-
=(-![]() ),
), ![]() =(0,2
=(0,2![]() ,0)
,0)
∴![]() ·
·![]() =
=![]() ·
·![]() =0
=0
∴PD⊥OE,PD⊥AC,∴PD⊥平面EAC
(Ⅱ)由(Ⅰ)知PD⊥EA,PD⊥EC,则∠AEC为二面角A-PD-C的平面角
∴![]() =(
=(![]() )
)![]() =(
=(![]() )
)
∴cos∠AEC=cos〈![]() ,
,![]() 〉=
〉= =-
=-![]()
(Ⅲ)由O为BD中点知,点B到平面PDC的距离为点O到平面PDC距离的2倍
又![]() =(
=(![]() ),
),
∴cos∠OED=cos〈![]() ,
,![]() 〉=
〉=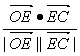 =-
=-![]() ,
,
所以点B到平面PDC的距离
d=3|![]() |sin∠OEC=2×
|sin∠OEC=2×![]()

 名校课堂系列答案
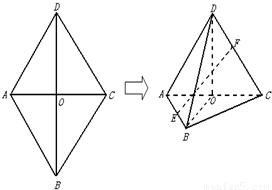
名校课堂系列答案 (2012•闸北区二模)如图,菱形ABCD中,AB=AC=1,其对角线的交点为O,现将△ADC沿对角线AC向上翻折,使得OD⊥OB.在四面体ABCD中,E在AB上移动,点F在DC上移动,且AE=CF=a(0≤a≤1).
(2012•闸北区二模)如图,菱形ABCD中,AB=AC=1,其对角线的交点为O,现将△ADC沿对角线AC向上翻折,使得OD⊥OB.在四面体ABCD中,E在AB上移动,点F在DC上移动,且AE=CF=a(0≤a≤1).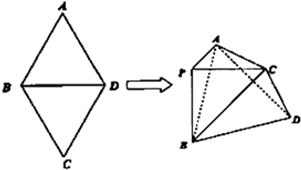 如图,菱形ABCD中,∠A=60°,把菱形ABCD沿对角线BD折成二面角A-BD-C,AC=BD,空间中的点P满足PA、PB、PC两两垂直,则下列命题中错误的是( )
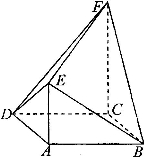
如图,菱形ABCD中,∠A=60°,把菱形ABCD沿对角线BD折成二面角A-BD-C,AC=BD,空间中的点P满足PA、PB、PC两两垂直,则下列命题中错误的是( )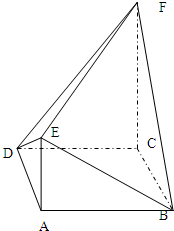 (2012•湘潭模拟)如图,菱形ABCD中,∠ABC=60°,AE⊥平面ABCD,CF⊥平面ABCD,AB=AE=2,CF=3.
(2012•湘潭模拟)如图,菱形ABCD中,∠ABC=60°,AE⊥平面ABCD,CF⊥平面ABCD,AB=AE=2,CF=3.