Question

（2012•闸北区二模）如图，菱形ABCD中，AB=AC=1，其对角线的交点为O，现将△ADC沿对角线AC向上翻折，使得OD⊥OB．在四面体ABCD中，E在AB上移动，点F在DC上移动，且AE=CF=a（0≤a≤1）．
（1）求线段EF的最大值与最小值；
（2）当线段EF的长最小时，求异面直线AC与EF所成角θ的大小．

Answer 1

分析：解一：（1）以O为坐标原点，如图建立空间直角坐标系，确定E，F的坐标，求出EF的长，利用配方法可求线段EF的最小值；
（2）a=

2

5

时，

EF

=(

3

5

，

3

5

，

3

5

)，

AC

=(0，1，0)，利用向量的夹角公式，可得异面直线AC与EF所成角θ的大小；
解二：（1）如图，过点F作FM∥DO，则FM=

3

2

a，求出EM的最小值，即可得到线段EF的最小值；
（2）过点E作EN∥AC，连接FN，则∠FEN为异面直线AC与EF所成角，在△EFN中，EN=

3

5

，FN=

6

5

，EF=

15

5

，由余弦定理可得异面直线AC与EF所成角θ的大小．

解答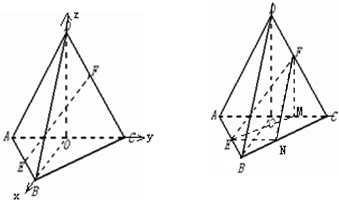：解一：（1）以O为坐标原点，如图建立空间直角坐标系O-xyz，…（1分）
则∵AB=AC=1，AE=CF=a（0≤a≤1），
∴E(

3

2

a，

a-1

2

，0)，F(0，

1-a

2

，

3

2

a)…（2分）
∴EF=

(1- a 2 )2+a2-a(1- a 2 )+( 3 2 a)2

=

5 2 (a- 2 5 )2+ 3 5

．     …（2分）
所以，当a=

2

5

时，线段EF的最小值为

15

5

．…（1分）
（2）a=

2

5

时，

EF

=(

3

5

，

3

5

，

3

5

)，

AC

=(0，1，0)，…（2分）
∴cosθ=|

EF • AC

| EF |•| AC |

|=

3 5

15 5 ×1

=

15

5

．…（3分）
所以异面直线AC与EF所成角θ的大小θ=arccos

15

5

．…（1分）
解二：（1）如图，过点F作FM∥DO，则FM=

3

2

a，…（2分）
在△AEM中，由余弦定理，得EM2=AE2+AM2-2AE•AMcos60°=

5

2

(a-

2

5

)2+

3

5

．…（3分）
所以，当a=

2

5

时，线段EF的最小值为

15

5

．     …（1分）
（2）过点E作EN∥AC，连接FN，则∠FEN为异面直线AC与EF所成角，…（1分）
∵EN∥AC，AB=AC=1，AE=

2

5

，∴EN=

3

5

，CN=

2

5

，
∵CF=

2

5

，∴FN∥DB
∵DB=

2

，∴FN=

6

5

在△EFN中，EN=

3

5

，FN=

6

5

，EF=

15

5

，…（2分）
由余弦定理可得cos∠FEN=

9 25 + 15 25 - 6 25

2× 3 5 × 15 5

=

15

5

，…（2分）
∴异面直线AC与EF所成角θ的大小θ=arccos

15

5

．…（1分）

点评：本题考查线段长的计算，考查线线角，考查利用空间向量解决立体几何问题，综合性强，属于中档题．