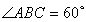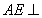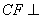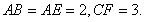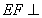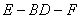题目内容
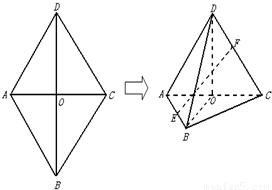
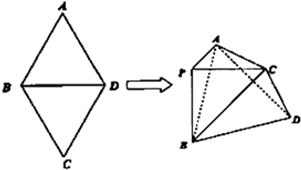 如图,菱形ABCD中,∠A=60°,把菱形ABCD沿对角线BD折成二面角A-BD-C,AC=BD,空间中的点P满足PA、PB、PC两两垂直,则下列命题中错误的是( )
如图,菱形ABCD中,∠A=60°,把菱形ABCD沿对角线BD折成二面角A-BD-C,AC=BD,空间中的点P满足PA、PB、PC两两垂直,则下列命题中错误的是( )分析:根据已知可判断出四棱锥A-BCD为正四面体,将四棱锥A-BCD补成一个正方体,建立空间坐标系,利用向量法,逐一判断四个答案的真假,可得答案.
解答: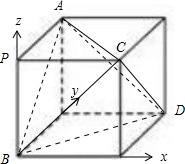 解:∵菱形ABCD中,∠A=60°,把菱形ABCD沿对角线BD折成二面角A-BD-C,AC=BD,
解:∵菱形ABCD中,∠A=60°,把菱形ABCD沿对角线BD折成二面角A-BD-C,AC=BD,
可得四棱锥A-BCD为正四面体
将四棱锥A-BCD补成一个正方体,如下图所示:
设正方体的棱长为1,易得向量
=(1,-1,1)为平面ABD的一个法向量;
=(-1,1,1)为平面BCD的一个法向量
设二面角A-BD-C的平面角为θ,则cosθ=
=
,故A正确;
=(1,0,0),∵
•
=1≠0,故PC的方向与平面ABD的法向量不垂直,故PC∥平面ABD不成立,故B不正确;
=(0,0,-1),
=(0,1,-1),∵cos<
,
>=
,故PB与CD所成角为45°,故C正确;
∵
=(1,1,0),故
•
=0,故PB⊥BD,故D正确;
故选B
 解:∵菱形ABCD中,∠A=60°,把菱形ABCD沿对角线BD折成二面角A-BD-C,AC=BD,
解:∵菱形ABCD中,∠A=60°,把菱形ABCD沿对角线BD折成二面角A-BD-C,AC=BD,可得四棱锥A-BCD为正四面体
将四棱锥A-BCD补成一个正方体,如下图所示:
设正方体的棱长为1,易得向量
| a |
| b |
设二面角A-BD-C的平面角为θ,则cosθ=
|
| ||||
|
|
| 1 |
| 3 |
| PC |
| PC |
| a |
| PB |
| CD |
| PB |
| CD |
| ||
| 2 |
∵
| BD |
| PB |
| BD |
故选B
点评:本题考查的知识点是命题的真假判断与应用,二面角的平面角及求法,空间线面关系的判定,构造空间坐标系,将线面夹角问题,二面角问题转化为向量夹角问题是解答的关键.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
 (2012•闸北区二模)如图,菱形ABCD中,AB=AC=1,其对角线的交点为O,现将△ADC沿对角线AC向上翻折,使得OD⊥OB.在四面体ABCD中,E在AB上移动,点F在DC上移动,且AE=CF=a(0≤a≤1).
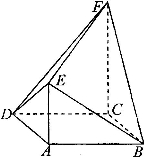
(2012•闸北区二模)如图,菱形ABCD中,AB=AC=1,其对角线的交点为O,现将△ADC沿对角线AC向上翻折,使得OD⊥OB.在四面体ABCD中,E在AB上移动,点F在DC上移动,且AE=CF=a(0≤a≤1).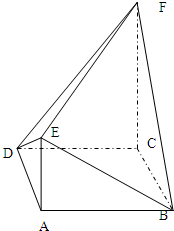 (2012•湘潭模拟)如图,菱形ABCD中,∠ABC=60°,AE⊥平面ABCD,CF⊥平面ABCD,AB=AE=2,CF=3.
(2012•湘潭模拟)如图,菱形ABCD中,∠ABC=60°,AE⊥平面ABCD,CF⊥平面ABCD,AB=AE=2,CF=3.