题目内容
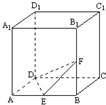 如图,正方体ABCD-A1B1C1D1中,E,F分别为AB与BB1的中点,
如图,正方体ABCD-A1B1C1D1中,E,F分别为AB与BB1的中点,(Ⅰ)求证:EF⊥平面A1D1B;
(Ⅱ)求二面角F-DE-C大小的正切值.
分析:(I)要证EF⊥平面A1D1B,只需证A1D1⊥EF,A1B⊥EF
(II)要求二面角F-DE-C大小的正切值,关键是找出二面角的平面角.延长DE、CB交于N,过B作BM⊥EN交于M,连FM,则∠FMB为二面角F-DE-C的平面角,故可求.
(II)要求二面角F-DE-C大小的正切值,关键是找出二面角的平面角.延长DE、CB交于N,过B作BM⊥EN交于M,连FM,则∠FMB为二面角F-DE-C的平面角,故可求.
解答:证明:(I)∵A1D1⊥平面A1B1BA,EF?平面A1B1BA,
∴A1D1⊥EF
∵A1B⊥AB1,EF∥AB1,
∴A1B⊥EF
∴EF⊥平面A1D1B;
解:(II)延长DE、CB交于N,∵E为AB中点,∴△DAE≌△NBE
过B作BM⊥EN交于M,连FM,
∵FB⊥平面ABCD
∴FM⊥DN,∴∠FMB为二面角F-DE-C的平面角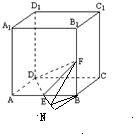
设AB=a,则BM=
=
又BF=
∴tan∠FMB=
=
,即二面角F-DE-C大小的正切值为
∴A1D1⊥EF
∵A1B⊥AB1,EF∥AB1,
∴A1B⊥EF
∴EF⊥平面A1D1B;
解:(II)延长DE、CB交于N,∵E为AB中点,∴△DAE≌△NBE
过B作BM⊥EN交于M,连FM,
∵FB⊥平面ABCD
∴FM⊥DN,∴∠FMB为二面角F-DE-C的平面角

设AB=a,则BM=
| BE•BN |
| EN |
| a | ||
|
| a |
| 2 |
∴tan∠FMB=
| FB |
| BM |
| ||
| 2 |
| ||
| 2 |
点评:本题以正方体为载体,考查线面垂直,考查面面角,关键是作出二面角的平面角.

练习册系列答案
相关题目

 如图,正方体ABCD-A1B1C1D1中,E,F分别为BB1和A1D1的中点.证明:向量
如图,正方体ABCD-A1B1C1D1中,E,F分别为BB1和A1D1的中点.证明:向量 如图,正方体ABCD-A1B1C1D1棱长为8,E、F分别为AD1,CD1中点,G、H分别为棱DA,DC上动点,且EH⊥FG.
如图,正方体ABCD-A1B1C1D1棱长为8,E、F分别为AD1,CD1中点,G、H分别为棱DA,DC上动点,且EH⊥FG. 如图,正方体ABCD-A1B1C1D1中,若E、F、G分别为棱BC、C1C、B1C1的中点,O1、O2分别为四边形ADD1A1、A1B1C1D1的中心,则下列各组中的四个点不在同一个平面上的是( )
如图,正方体ABCD-A1B1C1D1中,若E、F、G分别为棱BC、C1C、B1C1的中点,O1、O2分别为四边形ADD1A1、A1B1C1D1的中心,则下列各组中的四个点不在同一个平面上的是( ) 如图,正方体ABCD-A1B1C1D1中,E、F、G、H分别是所在棱的三等分点,且
如图,正方体ABCD-A1B1C1D1中,E、F、G、H分别是所在棱的三等分点,且