题目内容
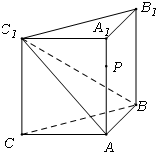 如图,侧棱垂直底面的三棱柱ABC-A1B1C1中,AB⊥AC,AA1+AB+AC=3,AB=AC=t(t>0),P是侧棱AA1上的动点.
如图,侧棱垂直底面的三棱柱ABC-A1B1C1中,AB⊥AC,AA1+AB+AC=3,AB=AC=t(t>0),P是侧棱AA1上的动点.(1)当AA1=AB=AC时,求证:A1C⊥平面ABC1;
(2)试求三棱锥P-BCC1的体积V取得最大值时的t值.
分析:(1)先证明AC1⊥A1C,再证明AB⊥平面AA1C1C,可得AB⊥AC1,利用线面垂直的判定定理,可得结论;
(2)确定点P到平面BB1C1C的距离等于点A到平面BB1C1C的距离,表示出三棱锥P-BCC1的体积,利用导数方法求最值.
(2)确定点P到平面BB1C1C的距离等于点A到平面BB1C1C的距离,表示出三棱锥P-BCC1的体积,利用导数方法求最值.
解答: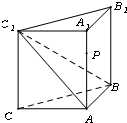 (1)证明:∵AA1⊥面ABC,∴AA1⊥AC,AA1⊥AB
(1)证明:∵AA1⊥面ABC,∴AA1⊥AC,AA1⊥AB
又∵AA1=AC,∴四边形AA1C1C是正方形,∴AC1⊥A1C.
∵AB⊥AC,AB⊥AA1,AA1,AC?平面AA1C1C,AA1∩AC=A,
∴AB⊥平面AA1C1C.
又∵AC1?平面AA1C1C,
∴AB⊥AC1,
∵AB,AC1?平面ABC1,AB∩AC1=A
∴A1C⊥平面ABC1.---(5分)
(2)解:∵AA1∥平面BB1C1C,∴点P到平面BB1C1C的距离等于点A到平面BB1C1C的距离
∴V=VP-BCC1=VA-BCC1=VC1-ABC=
t2(3-2t)=
t2-
t3(0<t<
),----(9分)
V'=-t(t-1),令V'=0,得t=0(舍去)或t=1,列表,得
∴当t=1时,Vmax=
.---(12分)
 (1)证明:∵AA1⊥面ABC,∴AA1⊥AC,AA1⊥AB
(1)证明:∵AA1⊥面ABC,∴AA1⊥AC,AA1⊥AB又∵AA1=AC,∴四边形AA1C1C是正方形,∴AC1⊥A1C.
∵AB⊥AC,AB⊥AA1,AA1,AC?平面AA1C1C,AA1∩AC=A,
∴AB⊥平面AA1C1C.
又∵AC1?平面AA1C1C,
∴AB⊥AC1,
∵AB,AC1?平面ABC1,AB∩AC1=A
∴A1C⊥平面ABC1.---(5分)
(2)解:∵AA1∥平面BB1C1C,∴点P到平面BB1C1C的距离等于点A到平面BB1C1C的距离
∴V=VP-BCC1=VA-BCC1=VC1-ABC=
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 3 |
| 3 |
| 2 |
V'=-t(t-1),令V'=0,得t=0(舍去)或t=1,列表,得
| t | (0,1) | 1 | (1,
| ||
| V' | + | 0 | - | ||
| V | 递增 | 极大值 | 递减 |
| 1 |
| 6 |
点评:本小题主要考查线面垂直,考查三棱锥的体积,考查化归与转化思想、数形结合思想、函数与方程思想及应用意识.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
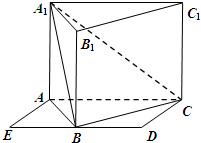 如图,侧棱垂直底面的三棱柱ABC-A1B1C1的底面ABC位于平行四边形ACDE中,AE=2,AC=AA1=4,∠E=60°,点B为DE中点.
如图,侧棱垂直底面的三棱柱ABC-A1B1C1的底面ABC位于平行四边形ACDE中,AE=2,AC=AA1=4,∠E=60°,点B为DE中点.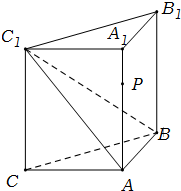 (2012•浙江模拟)如图,侧棱垂直底面的三棱柱ABC-A1B1C1中,AB⊥AC,AA1+AB+AC=3,AB=AC=t(t>0),P是侧棱AA1上的动点.
(2012•浙江模拟)如图,侧棱垂直底面的三棱柱ABC-A1B1C1中,AB⊥AC,AA1+AB+AC=3,AB=AC=t(t>0),P是侧棱AA1上的动点.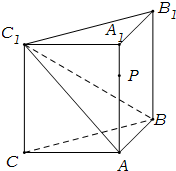 (2012•泉州模拟)如图,侧棱垂直底面的三棱柱ABC-A1B1C1中,AB⊥AC,AA1+AB+AC=3,AB=AC=t(t>0),P是侧棱AA1上的动点.
(2012•泉州模拟)如图,侧棱垂直底面的三棱柱ABC-A1B1C1中,AB⊥AC,AA1+AB+AC=3,AB=AC=t(t>0),P是侧棱AA1上的动点.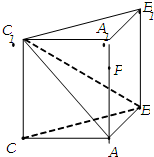 (2013•梅州二模)如图,侧棱垂直底面的三棱柱ABC-A1B1C1中,AB⊥AC,AA1+AB+AC=3,AB=AC=t(t>0).
(2013•梅州二模)如图,侧棱垂直底面的三棱柱ABC-A1B1C1中,AB⊥AC,AA1+AB+AC=3,AB=AC=t(t>0).