题目内容
12.在数轴上,实数$\frac{6{a}^{2}}{9+{a}^{4}}$对应的点为A,实数1对应的点为B,那么点A与点B的位置关系是怎样的?分析 作差得出$\frac{6{a}^{2}}{9+{a}^{4}}$-1=$\frac{6{a}^{2}-9-{a}^{4}}{9+{a}^{4}}$=-$\frac{({a}^{2}-3)^{2}}{9+{a}^{4}}$分类判断即可得出:点A与点B重合,点A在点B的右侧.的情况.
解答 解:∵$\frac{6{a}^{2}}{9+{a}^{4}}$-1=$\frac{6{a}^{2}-9-{a}^{4}}{9+{a}^{4}}$=-$\frac{({a}^{2}-3)^{2}}{9+{a}^{4}}$
∴①当a=$±\sqrt{3}$时$\frac{6{a}^{2}}{9+{a}^{4}}$-1=0,
∴点A与点B重合,
②当a$≠±\sqrt{3}$时,$\frac{6{a}^{2}}{9+{a}^{4}}$-1>0,
∴点A在点B的右侧.
点评 本题考查了作差法比较大小,难度较小,属于容易题.

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案
相关题目
3.若圆锥的内切球与外接球的球心重合,且内切球的半径为1,则圆锥的体积为( )
| A. | π | B. | 2π | C. | 3π | D. | 4π |
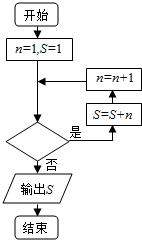 已知数列{an}中,a1=1,an+1=an+n,若利用如图所示的程序框图计算该数列的第10项的值S,则判断框内的条件是n≤9或n<10.
已知数列{an}中,a1=1,an+1=an+n,若利用如图所示的程序框图计算该数列的第10项的值S,则判断框内的条件是n≤9或n<10.