题目内容
已知正实数a、b、c满足条件a+b+c=3,
(Ⅰ) 求证: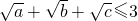 ;
;
(Ⅱ)若c=ab,求c的最大值.
解:(Ⅰ)由柯西不等式得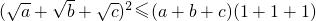
代入已知a+b+c=3,
∴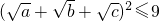 ,
,
∴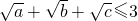
当且仅当=b=c=1,取等号.(3分)
(Ⅱ)由 ,
,
得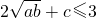 ,
,
若c=ab,则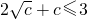 ,
,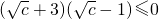 ,
,
所以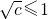 ,
,
即c≤1,当且仅当a=b=1时,
∴c有最大值1.(7分).
分析:(I)利用柯西不等式得(a2+b2+c2)(m2+n2+p2)≥(am+bn+cp)2得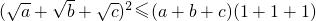 ,代入已知a+b+c=3即得;
,代入已知a+b+c=3即得;
(Ⅱ)由 ,得
,得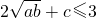 ,若c=ab,由(I)得
,若c=ab,由(I)得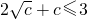 ,
,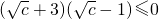 ,从而得出c≤1即得.
,从而得出c≤1即得.
点评:本题主要考查了一般形式的柯西不等式.证明不等式时,关键是如何凑成能利用一般形式的柯西不等式的形式,注意重要不等式中等号成立的条件.
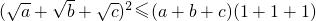
代入已知a+b+c=3,
∴
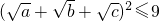 ,
,∴
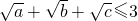
当且仅当=b=c=1,取等号.(3分)
(Ⅱ)由
 ,
,得
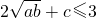 ,
,若c=ab,则
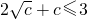 ,
,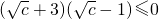 ,
,所以
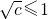 ,
,即c≤1,当且仅当a=b=1时,
∴c有最大值1.(7分).
分析:(I)利用柯西不等式得(a2+b2+c2)(m2+n2+p2)≥(am+bn+cp)2得
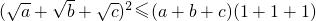 ,代入已知a+b+c=3即得;
,代入已知a+b+c=3即得;(Ⅱ)由
 ,得
,得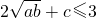 ,若c=ab,由(I)得
,若c=ab,由(I)得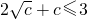 ,
,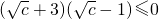 ,从而得出c≤1即得.
,从而得出c≤1即得.点评:本题主要考查了一般形式的柯西不等式.证明不等式时,关键是如何凑成能利用一般形式的柯西不等式的形式,注意重要不等式中等号成立的条件.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目